twierdzenia w trojkacie malinkaa: dlugosci bokow trojkata sa w stosunku2:3:4, a najkrotszy z bokow ma dlugosc a. znajdź promien okregu wpisanego w ten trojkat. oznaczylam boki jako 2x, 3x, 4x. 4x lezy naprzeciw największego kata \alpha . z twierdzenia cosinusa wynika że cos \alpha jest równy −1/4. 2. miary katow trojkata o obwodzie m sa rowne \alpha i \beta . znajdź dlugosc promienia okregu opisanego na tym trojkacie i pole trojkata.

Bogdan:

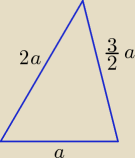
	1		3
2x = a ⇒ x =		a, 3x =		a, 4x = 2a
	2		2

	1		9		9
p − połowa obwodu trójkąta, p =		(2x + 3x + 4x) =		x =		a
	2		2		4

	5		3		3		1
p − a =		a, p −		a =		a, p − 2a =		a
	4		2		4		4

Pole trójkąta z wzoru Herona: P_Δ = √ (9a/4) * (5a/4) * (3a/4) * (a/4)

	PΔ
r − długość promienia okręgu wpisanego, PΔ = p*r ⇒ r =
	p

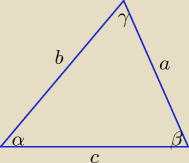
Bogdan: Zadanie 2. γ = 180^o − (α + β), sinγ = sin(α + β). R − długość promienia okręgu opisanego Z twierdzenia sinusów:

a		b		c
	= 2R,		= 2R,		= 2R
sinα		sinβ		sinγ

a = 2Rsinα, b = 2Rsinβ, c = 2Rsin(α + β), m = a + b + c ⇒ m = 2R(sinα + sinβ + sin(α + β)) ⇒ R = ...

	1		a*b*c
Pole: P =		absinγ, P =		, P = 2R2sinα*sinβ*sinγ
	2		4R