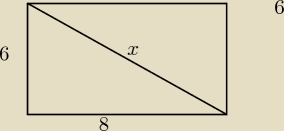
Wysokość ostrosłupa Mateusz: Na rysunku przedstawiony jest ostrosłup , którego podstawa jest prostokąt o wymiarach 8 cm x 6 cm. Stosunek długości krawędzi bocznej tego ostrosłupa do długości przekątnej jego podstawy jest równy 2:1. a) Oblicz wysokość tego ostrosłupa. b) Czy możliwe jest umieszczenie w tym ostrosłupie stożka o promieniu podstawy 3 cm i wysokości ^49√15₁₀ Moje obliczenia : 6 + 8² = x² x² = 100 x = 10

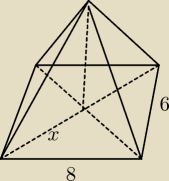
Mateusz: Rysunek pomocniczy Według mnie x to przekątne

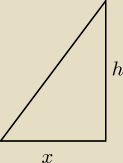
ICSP: Dwa pytania: 1. Ile wynosi krawędź boczna 2. Jakiego rodzaju jest trójkąt który zawiera : połowę przekątnej podstawy, wysokość, krawędź boczną? Jeżeli możesz narysuj go(nawet nie musi być trójwymiarowy. Wystarczy normalny trójkąt)

Mateusz: 1. "Stosunek długości krawędzi bocznej tego ostrosłupa do długości przekątnej jego podstawy jest równy 2:1. więc wydaje mi się że 20 cm 2. Powinien być to trójkąt prostokątny

ICSP: czyli ustalone. Krawędź boczna ma 20 ( nie rozumiem dlaczego brak tej danej na rysunku? Jeżeli x jest przekątną podstawy wtedy jest źle zaznaczone na tym rysunku. Zauważ że nie cały x jest w tym trójkącie.

Mateusz: Czyli teraz z twierdzenia Pitagorasa powinno mi wyjść że: ¹₂ x² + h² = l (krawędz boczna) 5² + h² = 20² h² = 400 − 25 h² = 375 h = 19,36 Czy to jest dobrze

ICSP: przyczepię się do dwóch rzeczy.

	1
pierwszą jest zapis		x2. Jest on błędny ponieważ według tego zapisu najpierw podnosimy
	2

10² a później dopiero dzielimy przez 2.

	1
Prawidłowy zapis to (		x)2.
	2

5² + H² = 400 H² = 20² − 5² = (20−5)(20+5) = (15)(25) H = √(15)(25) = 5√15. − i właśnie ten zapis H jest drugą rzeczą do której się przyczepię. Reszta ok.

Mateusz: Jak teraz obliczyć b)

ICSP: Stożek możemy umieścić w ostrosłupie gry : wysokość stożka jest mniejsza od wysokości ostrosłupa oraz gdy podstawa stożka mieści się w podstawie ostrosłupa. Potrzebne dane: Długość średnicy podstawy stożka (musi być ≤ 6 (wystarczy wykazać tylko dla krótszej krawędzi co jest zresztą logiczne). Druga potrzebna dana to wysokość. Jest ona podana w zadania. Wystarczy napisać te warunku w formie matematycznej.

Mateusz: No więc chyba o to chodzi Średnica : 3≤6 Wysokość : ^49√15₁₀≤5√15

ICSP: promień ≠ średnicy.

Mateusz: Aha to średnica wynosi 6 cm czyli i tak zmieści się

ICSP: na styk ale się zmieści. Jeszcze tylko Eta potwierdzi i będzie git.