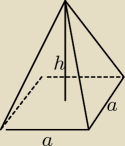 Zad. Wyznacz wielomian V opisujacy objetosc ostroslupa prawidlowego czworokatnego o krawedzi
podstawy a i wysokosci h jako funkcje x. Podaj dziedzine tej funkcji.
a=x+3, h=3(x2−6x+9)
Zad. Zapisz wielomian w postaci sumy.
a)(5x+1)3
b)(x−√2)3
Zad. Korzystajac ze wzoru Newtona, podaj rozwiniecie (a+b)7 oraz (a−b)7
Prosze o dokladne rozpisanie tych zadan tak, aby nawet takie matematyczne beztalencie jak ja
zdolalo cos pojac. Z gory bardzo dziekuje
Zad. Wyznacz wielomian V opisujacy objetosc ostroslupa prawidlowego czworokatnego o krawedzi
podstawy a i wysokosci h jako funkcje x. Podaj dziedzine tej funkcji.
a=x+3, h=3(x2−6x+9)
Zad. Zapisz wielomian w postaci sumy.
a)(5x+1)3
b)(x−√2)3
Zad. Korzystajac ze wzoru Newtona, podaj rozwiniecie (a+b)7 oraz (a−b)7
Prosze o dokladne rozpisanie tych zadan tak, aby nawet takie matematyczne beztalencie jak ja
zdolalo cos pojac. Z gory bardzo dziekuje 
| ||||||||
(a+b)n = n∑k=0 | akbn−k. | |||||||
|
|
|
|
| ||||||||||||||||||||||||||||||||||||
(a+b)7 = | a0b7 + | a1b6 + | a2b5 + ... + | a6b1 + | a7b0. | |||||||||||||||||||||||||||||||||||
|
| |||||||||||||||
Teraz musisz policzyć każdy | , ..., | korzystając ze wzoru: | ||||||||||||||
| n! | ||||||||
= | . | ||||||||
| k!(n−k)! |
