Całeczka do sprawdzenia Kanapka: Mógłby mi ktoś powiedziec czy dobrze policzyłam całkę ∫ln²x bo zrobiłam najpierw przez części potem znów przez częsci i wyszło mu ln²x*−2lnx+2x +C

AS: Pokaż tok obliczeń.

Trivial: Wystarczy policzyć pochodną z wyniku, żeby sprawdzić czy jest OK.

Kanapka: Dzięki wiem ze juz x zgubiłam

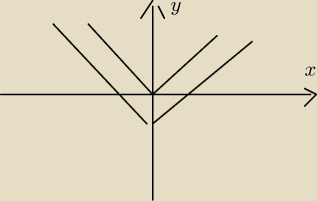
Kanapka: A mam do was takie pytanie bo roziwązuje teraz zadaie oblicz pole obszaru zawartego pomiędzy krzywymi y=x²=2 i y=x² i jak narysowałam to na wykresie to nie chce mi wyjść obszar zamknięty < ta weższ to jest y=x² a to szersza to x²−2 bo pierwsze tak jak zawsze zrobiłąm tableke i wpsiałam −3,−2,−1,0,1,2,3 i tak dla obu podkładałam pod x te liczby

Trivial: Bo te funkcje nie mają punktów przecięcia. Jesteś pewna, że wszystko dobrze przepisane?

Kanapka: To jest zadanie z egzaminu a nie wiesz czy ja cos takiego moge wyliczyc bo skoro nie mam czyli nie moge obliczyć obszaru wspólnego

Trivial: Może był podany przedział.

Kanapka: Być może ale oki a jeśli mogę ci tylko jedno pytanie zadać byłabym bardzo wdzięczna i zebys na nie odpowiedział

Trivial: To znaczy?

Kanapka: Oblicz objętość y=x√cosx gdzie x<lub równe pi/2 to jaki ja mam tu wziąść obszar całkowania?

Trivial: Ale to chyba zadanie na: Oblicz objętość bryły powstałej przez obrót funkcji wokół osi Ox: y = x√cosx Bez tego czerwonego kawałka zadanie nie ma sensu.

Trivial:

	π
i pewnie 0≤x≤		... ← granice całkowania.
	2

Ale jeśli nie ma tego 0, to znów nie ma sensu.

Kanapka: Napewno tak były bo o bryły obrotowe chodzi

Kanapka: czyli zawsze gość musi mi podac na egzaminie tak ze od 0 do pi/2

Kanapka: a jak podniose √cosx do kwadratu to pierwiastek mi sie z kwadratem skróci i zostanie samo cosx?

Trivial: Nie zawsze. Jeżeli masz bryłę, która jest ograniczona od razu przez dziedzinę, np. y = √4−x² to granice są niejako od razu ustalone (w tym przykładzie −2≤x≤2), chyba że zaznaczono inaczej. Ale w większości przykładów podadzą gotowe granice. Najlepiej narysować przed rozwiązaniem jeśli ma się czas − wtedy nie będzie problemów.

Trivial: Tak, ale tam jest jeszcze x przed pierwiastkiem.

Kanapka: Dzięki za rade ja sobie tam zawsze rysuje a co z tym moim pierwiastem z cos do kwadratu zostanie sam cos? bo sie pogłubiłam

Trivial: (√x)² = x. √x² = |x|.