Geometria analityczna humanista17: Mając dane punkty A = (−4,6), B = (4,2) wyznacz na osi x taki punkt C aby ∡ACB = 90^o.

humanista17: Podpowie ktoś jak się za to zabrać?

ICSP: 1. Liczysz długośc boku |AB| 2. Liczysz długości boków |AC| oraz |BC| podpowiem że punkt C ma współrzędne : C(x;0) 3. Twierdzenie Pitagorasa aby obliczyć x.

mamba: Można tutaj skorzystać z iloczynu skalarnego i bardzo szybko wyjdzie Dla kąta prostego cos= 90*, czyli 0 a więc iloczyn skalarny 2 wektorów musi być równy 0 v₁=CA=[−4−x, 6] v₂=CB=[4−x, 2] v₁ o v₂=0 (−4−x)*(4−x)+6*2=0 −1*(4+x)*(4−x)+12=0 −(16−x²)+12−= −16+x²+12=0 x²−4=0 => (x−2)*(x+2)=0 x₁=2 v x₂=−2 1. Dla x₁=2 punkt C ma współrzędne C(2, 0) 2. Dla x₁=−2 punkt C ma współrzędne C(−2, 0)

Gustlik: mamba, właśnie chciałem tę metodę tu zamieścic, niemniej kolejna pożyteczna metoda z iloczynem skalarnym wywalona z podstaw nauczania. CHORY PROGRAM !

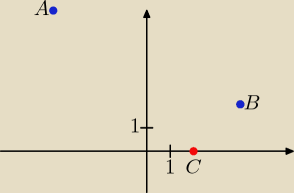
Bogdan: Można i tak: A = (−4, 6), B = (4, 2), C = (x, 0) Wyznaczamy współczynniki kierunkowe prostych zawierających punkty A i C oraz B i C:

	−6		−2
aAC =		, aBC =		, x≠−4 i x≠4.
	x + 4		x − 4

Korzystamy z warunku prostopadłości prostych: a_AC * a_BC = −1

−6		−2
	*		= −1 ⇒ x2 = 4 ⇒ x = −2 lub x = 2
x + 4		x − 4

Odp.: C₁ = (−2, 0), C₂ = (2, 0)

Patryk: nie można zrobic tak ? 1 znaleźć obojętnie jakis punkt C na osi ox 2.wyznaczyć równanie prostej AC 3. znaleźć równaie prostopadłe do rónania AC i przechodzącego przez punkt B

Bogdan: Patryku, właśnie to pokazałem. Nie potrzeba wyznaczać równania prostych, wystarczą same współczynniki kierunkowe tych prostych.

Patryk: aha