. bigL: doprowadź do najprostszej postaci następujące wyrażenia wykorzystując podane założenia. d)2|x+1|−|3+3x| , x≥−1 2|x+1|−|3+3x| =2x+2−3−3x=−x−1=−(x+1) dobrze?

bigL: sprawdzi ktoś czy to jest dobrze? I jak zrobić przykład poniżej?

x2−1
	+|1−x|, x∊(−∞,−1)
|x|−1

.

x2−1
	+|1−x|=
|x|−1

bigL: proszę o sprawdzenie podpunktu d) i wskazówkę jak zrobić przykład post wyżej

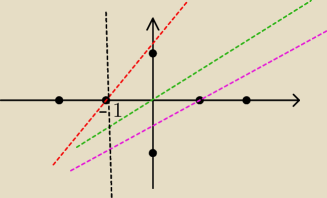snake: Pokaże na przykładzie: Rysujemy funkcje na wykresie pod wartością bezwzględną i zaznaczamy ich miejsca zerowe na wykresie. x+1=> x=−1 3+3x=>x=−1 Tutaj akurat funkcje mają to samo miejsce zerowe co dla nas lepiej Interesuje nas przedział <−1, +∞) Jak widzimy od<−1 +∞ funkcja przyjmuje wartości dodatnie. Jeśli przyjmuje dodatnie to opuszczamy wartość bezwzględną bez zmiany znaków: 2|x+1|−|3+3x| => 2(x+1)−(3+3x) => 2x+2−3−3x => −x−1 => −(x+1) Odp. Rozwiązaniem tego działania jest −(x+1). Zobaczmy jeszcze inny przykład.

x2−1
	+|1−x|
|x|−1

Tutaj musimy założyć, że |x|−1≠0, czyli |x|≠1 => x≠1 v x≠−1, ale że mamy przedział (−∞,−1) to możemy to ominąć Miejsca zerowe: 1−x => x=1 x => x=0 widzimy, że w (−∞,−1) przyjmują wyłącznie wartości ujemne, więc przed wartościamy bezwzględnymi dajemy minusy i likwidujemy wartośći.

x2−1		(x−1)(x+1)		x−1
	−(1−x)=		−(1−x)=		−(1−x)=−(x−1)−(1−x)=−x+1−1+x=0
−x−1		−(x+1)		−1

Odp. Rozwiązaniem działania jest liczba 0

bigL: To ze sprawdzeniem to dobrze zrobiliśmy Ale z tym przykładem co podałem to rozwiązałeś źle, ale już się z nim uporałem i pytałem na innym forum czy zrobiłem dobrze. W nim powinno wyjść 2(1−x) gdzieś się pomyliłeś zapewne. Ale dziękuje za odp, pozdrawiam.

snake: Tak zapewne gdzieś się walnąłem w znakach ale nei chce mi sie szukać

snake : Już wiem tam było | czyli −x+1, czyli funkcja malejaca a wiec przyjmei wartosci dodatnie i wyjdzie −2x+2