Proszę o pomoć w równaniu liniowym.
mamba: Wyznacz równanie prostych stycznych do okręgu x2+y2=4 przechodzących przez punkt P(4, −2).
Ja to robię tak:
1. Wyznaczam równanie prostej przechodzącej przez punkt P.
−2=4a+b => b=−(2+4a)
y=ax−(2+4a)
2. Odległość punktu O(0, 0) od prostej y=ax−(2+4a) równia się 2(r2=4). Tylko mam problem z
zapisaniem funkcji linowej w postaci równania liniowego Ax+Bx+C=0. Mógłby mi ktoś wytłumaczyć
jak sprowadzić tą funkcję: y=ax−(2+4a) . Przenoszenie na druga strone nic nic daje bo wszystko
się redukuje w liczniku równania na odległość punktu.
3 wrz 00:22
ICSP: y = ax − (2+4a) Tak napisałeś ⇔ ax − y − (2+4a) = 0
A = a
B = −1
C = −(2+4a)
3 wrz 00:43
ICSP: i teraz wstawiamy :
| | | a * 0 + −1 * 0 −(2+4a)| | | 2+4a | | 4 | |
2 = |
| ⇔ 2 = |
| ⇔ a = 0 v a = − |
| |
| | √a2+1 | | √a2+1 | | 3 | |
dla a = 0 otrzymujemy prostą y = −2 która jest funkcją stałą.
| | 4 | | 4 | | 10 | |
dla a = − |
| otrzymujemy prostą: y = − |
| x + |
| |
| | 3 | | 3 | | 3 | |
Mogłem się pomylić bo już przysypiam.
3 wrz 00:52
ICSP: dobra niech będzie. Dam

jako oznakę że dobrze zrobiłem

3 wrz 01:01
mamba: To zadanko można jeszcze zrobić na okręgach ale to szybszy sposob niż bawić się w układy równań

3 wrz 01:20
ICSP: jak się wyśpię to spróbuję dodać jeszcze jeden sposób

3 wrz 01:26
mamba: Ej a o co chodzi we wzorze na równanie prostej prostopadłej do wektora →v = [p,q] i
przechodzącej przez punkt (x0,y0)? Jak to zrobić jeśli np mam jakąs tam prosta i 2 punkty
lezace na tej rprostej. Można wyliczyć S i wspolczynnik kierunkowy obrocic z minusem i
podstawisc punkt S a z tym wektorem t oo co biega?
3 wrz 01:31
ICSP: wektorów nie używam

Może
Trivial odpowie ci na to pytanie.
3 wrz 01:33
mamba: Aha może akurat zajrzy

3 wrz 01:34
Trivial:
Mógłbyś podać ten wzór, bo nie wiem jak on wygląda?
3 wrz 12:19
mamba: Proszę bardzo tutaj masz ten wzór:
p (x− x0)+ q(y− y0) = 0.
Chyba już wiem o co biega. Jak ma się punkty na lezące do prostej to liczymy wektor tych 2
punktów i środek odcinka AB:
S=(1−62, 4+32)
S=(−52, 72)
A = (1,4) i B = (− 6,3 ), więc wektor AB=v=[−1−6, 3−1], czyli v=[−7, 1]
Teraz podstawiamy do wzorku:
−7*(x+52)−1*(y−72)=0
m prostą
− 7x−352−y+72=0, co po sprowadzeniu do postaci y=ax+b otrzymujemy
y=−7x−14, co jest prosta prostopadla przechodzaca przez S do prostej przechodzaccej przez A i
B.
3 wrz 14:49
ICSP: Wyznacz równanie prostych stycznych do okręgu x
2+y
2=4 przechodzących przez punkt P(4, −2).
najpierw wyznaczamy prostą:
−2 = 4a + b ⇔ b = −2 −4a
czyli prosta ma równanie: y = ax − 2 − 4a
zapisujemy układ równań:
y = ax − 2 − 4a
x
2 + y
2 = 4
teraz pierwsze równanie podnosimy do kwadratu:
y
2 = a
2x
2 + 4 + 16a
2 − 4ax − 8a
2x + 16a.
Porządkujemy:
y
2 = a
2x
2 −x(4a+8a
2) + 16a
2 + 16a + 4
Teraz wstawiamy to do pierwszego równania:
x
2 + a
2x
2 −x(4a+8a
2) + 16a
2 + 16a + 4 = 4
x
2(a
2+1) −x(4a+8a
2) + 16a
2 + 16a = 0
liczymy deltę:
Δ = (4a+8a
2)
2 −4(a
2+1)(16a
2+16a) = 16a
2 + 64a
3 + 64a
4 − 4(16a
4 + 16a
3 + 16a
2 + 16a) =
16a
2 + 64a
3 + 64a
4 − 64a
4 − 64a
3 − 64a
2 − 64a = −48a
2 − 64a
| | 4 | |
−48a2 − 64a = 0 ⇔ −a(48a + 64) = 0 ⇔ a = 0 v a = − |
| . |
| | 3 | |
3 wrz 15:13
snake:
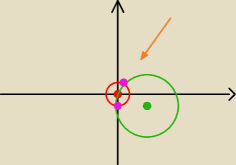
Tak to jest właśnie ten inny sposób dość żmudny i łatwo o pomyłkę w działaniu

Ja pokaże jeszcze inny.
1. Liczymy odległość |PO| , gdzie P(4, −2) i O(0, 0)
√(0−4)2+(0+2)2=
√16+4=
√20
|PO|
2=r
2= (
√20)
2=20
2. Robimy równanie okręgu o środku w punkcie P(4, −2) i promieniu równym |PO|.
(x−4)
2+(y+2)
2=20
3. Bierzemy część wspólną okręgu 1 i 2 dzięki czemu wyliczymy punkty styczności.
| ⎧ | x2+y2=4 | |
| ⎩ | (x−4)2+(y+2)2=20 |
|
Nie liczyłem tym sposobem bo mi się nie chciało ale powinno wyjść

Jak amsz casz to możesz
obliczć.
3 wrz 16:05
mamba: Tak ja zrobiłem tym sposobem co snake i znam go. Jest bardzo przydatny w wielu typach zadań
warto zapamietac

3 wrz 16:06
ICSP: ja tak się spytam czy odległość różowego punktu od zielonego jest równa odległości czerwonego
od zielonego?
i drugie pytanie:
czy te różowe punkty są miejscami styczności?
3 wrz 16:11
mamba: 1. Nie są równe. Odległość czerwonego od zielonego to ma być promień nowego koła. Ale na tym
rysunku tak to wygląda jak by były równe

2. Tak myślę, że snake właśnie po przez te 2 różowe kropki chciał pokazać punty stycznośći

ale nie jestem pewien

Niech wypowie się autor

3 wrz 16:21
snake: Tak mamba dobrze myślisz a twoje słowa prawdę głoszą


3 wrz 16:28
Trivial:
A nie prościej wyprowadzić wzór?

Jeżeli:
(x−S
x)
2 + (y−S
y)
2 = R
2 P = (P
x, P
y).
x
0 = P
x − S
x y
0 = P
y − S
y k =
√(x02+y02)/R2 − 1
Wtedy:
| | x0+ky0 | | x0−ky0 | |
a1 = |
| a2 = |
| |
| | y0−kx0 | | y0+kx0 | |
Wiedza tak oczywista, że bez dowodu.

3 wrz 18:36
 jako oznakę że dobrze zrobiłem
jako oznakę że dobrze zrobiłem 


 Może Trivial odpowie ci na to pytanie.
Może Trivial odpowie ci na to pytanie.

 Tak to jest właśnie ten inny sposób dość żmudny i łatwo o pomyłkę w działaniu
Tak to jest właśnie ten inny sposób dość żmudny i łatwo o pomyłkę w działaniu  Ja pokaże jeszcze inny.
1. Liczymy odległość |PO| , gdzie P(4, −2) i O(0, 0)
√(0−4)2+(0+2)2=√16+4=√20
|PO|2=r2= (√20)2=20
2. Robimy równanie okręgu o środku w punkcie P(4, −2) i promieniu równym |PO|.
(x−4)2+(y+2)2=20
3. Bierzemy część wspólną okręgu 1 i 2 dzięki czemu wyliczymy punkty styczności.
Ja pokaże jeszcze inny.
1. Liczymy odległość |PO| , gdzie P(4, −2) i O(0, 0)
√(0−4)2+(0+2)2=√16+4=√20
|PO|2=r2= (√20)2=20
2. Robimy równanie okręgu o środku w punkcie P(4, −2) i promieniu równym |PO|.
(x−4)2+(y+2)2=20
3. Bierzemy część wspólną okręgu 1 i 2 dzięki czemu wyliczymy punkty styczności.
 Jak amsz casz to możesz
obliczć.
Jak amsz casz to możesz
obliczć.

 2. Tak myślę, że snake właśnie po przez te 2 różowe kropki chciał pokazać punty stycznośći
2. Tak myślę, że snake właśnie po przez te 2 różowe kropki chciał pokazać punty stycznośći  ale nie jestem pewien
ale nie jestem pewien  Niech wypowie się autor
Niech wypowie się autor 


 Jeżeli:
(x−Sx)2 + (y−Sy)2 = R2 P = (Px, Py).
x0 = Px − Sx y0 = Py − Sy k = √(x02+y02)/R2 − 1
Wtedy:
Jeżeli:
(x−Sx)2 + (y−Sy)2 = R2 P = (Px, Py).
x0 = Px − Sx y0 = Py − Sy k = √(x02+y02)/R2 − 1
Wtedy:
