Faunkcja liniowa, zadanie. Agata: Podaję tu zadanie, które nie wiem jak zacząć. Nie wiem, czy mam te wszystkie funkcje narysować na jednym wykresie i proszę o pomoc. Z góry dziękuję Dana jest funkcja określona wzorem: a) f(x) = 2x − 3 b)f(x) = − ¹₂ + 1

	⎧	−2x + 1, x∊1
c)	⎨	2, −1≤x≤1
	⎩	2x+1, x>1

Naszkicuj jej wykres, podaj jej własności, oblicz wartość funkcji dla argumentów 2¹₂, wyznacz argument, dla którego wartość funkcji wynosi 4, sprawdź, zy punkt o współrzędnych (1, 1/2) należy do wykresu funkcji.

Agata: w przykładzie b) jest wzór −¹₂x +1 , pomyliłam się

Eta: Napisz porządnie treść zadań

Eta: w c) −2x+1 , x€ ............

Eta: https://matematykaszkolna.pl/strona/44.html narysuj prostą w podpunktach a) b)

Agata: cały przykład c podaję, chociaż to, co napisałam jest dobrze, przynajmniej tak myślę :

⎧	−2x+1, x∊1
⎨	2, −1≤x≤1
⎩	2x+1, x>1

Sorry za bałagan, jestem w stresie, że zapomniałam jak to zrobić, co dowodzi dość niskiemu poziomowi mojej wiedzy z matematyki

Eta: myślę,że c) jest tak: { −2x+1 , x< −1 { 2 −1≤x≤ 1 { 2x+1 , x>1

Agata: Nie wiem, czy źle przepisałam z tablicy, czy nauczyciel źle nam podał treść, ale niestety tak właśnie mam w zeszycie Ok, zrobiłam sobie przykład c, wybrałam liczby z przedziałów, które zostały podane, i rysuję punkty na tym samym wykresie? Bo resztę zadania umiem zrobić, chodzi mi tylko o początek Dzięki za pomoc.

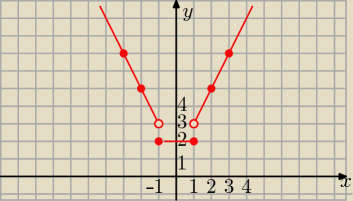Eta: c) rysujemy wykres częściami 1) f(x)= −2x+1 dla x€( −∞, −1) −−−− wykresem jest półprosta bez początku znajdujemy kilka punktów dla tej półprostej x= −1 to y= −2*(−1)+1= 2+1=3 ( −1, 3) −− ten punkt nie należy do wykresu x= −2 y= −2*(−2)+1= 4+1=5 ( −2, 5) −−− ten należy x= =3 y= −2*(−3)+1= 7 (−3, 7) −−− należy itd 2/ dla x€<−1,1> f(x)= 2 −−− to funkcja stała wykresem jest odcinek o końcach w punktach ( −1,2) (1, 2) 3) dla x>1 f(x)= −2x+1 ( wykresem jest półprosta bez początku znajdujemy kilka jej punktów x=1 to y= −2x+1= ....... x= 2 to y= .... x= 3 y=..... itd.. teraz odpowiedz na zadane pytania:

	1
dla x = 2		>1
	2

	1		1
to z podpunktu 3) f(2		) = −2(2		)+1=......
	2		2

f(x)= 4 <=> 2x+1=4 lub −2x+1=4 czyli x= 1,5 lub x=−1,5 −−−−− co widać też z wykresu

	1
punkt (1,		) ............ nie należy do wykresu
	2

przeanalizuj to zadanie i poćwicz podobne przykłady powodzenia