Obliczyć całkę Artek: ∫∫_s (8−2z)ds z: 4− 1/2x² −1/2y² z>0 Moje zadanie z egzaminu, którego oczywiście nie zrobiłem. Kompletnie nie wiem od czego tu trzeba zacząć Liczę na waszą pomoc

Artek: pomoże ktoś ?

Trivial: ∬_S(8−2z)dS

	1		1
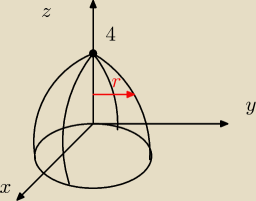
S: z=4−		x2−		y2, z>0
	2		2

Powierzchnia jest paraboloidą 'uciętą od dołu'.

	1
z = 4−		(x2+y2)
	2

Gdy powierzchnia jest wykresem funkcji g, aby znaleźć współrzędne wektora normalnego do tej powierzchni możemy skorzystać ze wzoru:

	∂g		∂g
N(x,y) = (−		(x,y), −		(x,y), 1)
	∂x		∂y

Tutaj g to nasze z, a więc:

∂z		∂z
	= −x		= −y
∂x		∂y

N = (x, y, 1) ||N|| = √x² + y² + 1 Przechodzimy na współrzędne biegunowe.

	1
z = 4−		r2
	2

||N|| = √r² + 1 Ustalamy granice całkowania. Dla z = 0:

1
	r2 = 4
2

r² = 8 r = 2√2 Dla z = 4: r = 0. (r, φ) ∊ Δ = [0, 2√2]×[0, 2π] Zamieniamy całkę powierzchniową na podwójną.

	1
∬S(8−2z)dS = ∬Δ[8−2(4−		r2)]*√r2 + 1drdφ = ∬Δr2√r2 + 1drdφ =
	2

= 2π*∫₀^2√2 r²√r² + 1dr

	r4+r2		dr
∫r2√r2+1dr = ∫		dr = (Ar3+Br2+Cr+D)√r2+1 + k∫
	√r2+1		√r2+1

... Czy to aby jest dobrze przepisane? Strasznie dużo liczenia.

to sie rusza: chyba zapomniałeś o jakobianie

piotr:

	1
∫r3 √1 + r2 dr =		(r2 + 1)3/2(3 r2 − 2) + C
	15