Trivial ICSP: Trivial oprócz niepohamowanej chęci zabijania komarów posiadasz jakieś zadania z liczb C? Oczywiście posługujemy się międzynarodowymi oznaczeniami.

Trivial: Complex? Masz zadanie: Wyprowadź wzór na pierwiastek z dowolnej liczby zespolonej z.

Trivial: Pierwiastek oczywiście kwadratowy.

ICSP: ale chodziło mi o proste zadanie.

Trivial: Ale to jest proste zadanie. Nie wymaga głębszej znajomości liczb zespolonych... To może pomogę. √z = w ⇔ w² = z z = a + ib w = x + iy ...

Trivial: To jak ICSP, próbujesz? Proste zadanko.

ICSP: spróbuję ale jutro i nie wydaje mi się aby to było proste zadanko.

ICSP: x² + 2xyi − y² = a + ib możemy to zapisac następująco: x² − y² = a 2xy = b i nie mam pomysłu co dalej Nawet jeśli zacznę wyznaczać to nie wyznaczę całej liczby tylko np. częsc y albo x.

Trivial: Jak to część?

	b
y =
	2x

Podstawić i liczysz...

ICSP:

	b2
x2 −		= a
	4x2

4x⁴ −4x²a − b² = 0 t = x² 4t² − 4ta −b² = 0 Δ = 16a + 16b² = 16(a+b²) √Δ = 4√a+b²

	4 + 4√a+b2		1 + √a + b2
t1 =		=
	8		2

	1 − √a+b2
t2 sprężenie pierwszego :
	2

	1 ± √a + b2
x = ±		Ten zapis jest poprawny?
	2

	b
y =
	1 ± √a + b2   2±   2

	1 ± √a + b2		b
czyli x = ±		+ iy =
	2		1 ± √a + b2   2±   2

Trivial: Witaj ICSP. 4t² − 4at − b² = 0 Zapominasz wszędzie o a. Ale tak właśnie trzeba rozwiązać. y można potem uprościć.

Trivial: A jeśli chodzi o zapis z ± to nie do końca, bo jednemu x odpowiada jeden y. I jeszcze zapomniałeś o pierwiastku przy przejściu z t na x. To zadanie jest dużo prostsze z tym a i pierwiastkiem.

ICSP: zapomniałem a podnieś do kwadratu

	1 ± √|z|
x = ± √
	2

Teraz dobrze?

ICSP:

	1 + |z|		1 − |z|
nie x = ± √		v x = ± √
	2		2

Trivial: 4t² − 4at − b² = 0 Δ = 16a² + 16b² = 16(a²+b²) √Δ = 4√a² + b² = 4|z|

	4a ± 4|z|		a ± |z|
t =		=
	8		2

ale t ≥ 0 więc:

	a + |z|
t =
	2

...

ICSP: dlaczego t≥0 ?

Trivial: bo t = x². liczby x, y, a, b są rzeczywiste.

ICSP: rzeczywiście Sprytna pułapka x = ± √(a + |z|)/2

	b
y =
	2± √(a + |z|)/2

ICSP: Teraz już jest dobrze?

Trivial: x ok, ale nie można sobie tak liczyć y, bo nie wiadomo dla którego x jest dany y.

ICSP: tzn ze trzeba wprowadzić funkcję sgn która uzależni x od y? Nie za bardzo rozumiem co chcesz powiedzieć przez "nie można tak sobie liczyć y"

Trivial: Rozwiązaniem równania są dwie pary (x, y) Przy twoim zapisie można skonstruować 4 takie pary, a więc zapis niekonsekwentny. O to mi chodziło. I tak, wprowadza się sgn aby wyliczyć y i jeszcze można przekształcić tak, aby y był trochę prostszy.

ICSP:

	b√2(a+|z|)
y =		. Dobrze przekształcone?
	2(a+|z|)

Trivial: x = sgn(x)√¹₂(a+|z|)

	b		1
y =		= sgn(x)sgn(b)|b|
	2sgn(x)√12(a+|z|)		√2(a+|z|)

1		a−|z|		a−|z|		|z|−a
	=		=		=
a+|z|		a2−|z|2		a2−a2−b2		b2

1		1		1		|z|−a		√12(|z|−a)
	=(		*		)1/2=(		)1/2=
√2(a+|z|)		2		a+|z|		2b2		|b|

	√12(|z|−a)
y = sgn(x)sgn(b)|b|*		= sgn(x)sgn(b)√12(|z|−a).
	|b|

	b
Ale i tak chyba łatwiej jest zapamiętać po prostu wzór na x a potem wyliczyć y =		.
	2x

ICSP: zdecydowanie łatwiej jest zapamiętać wzór na x Akurat wyznaczenie tego wzorku już mniej więcej rozumiem. Możesz dać następne zadanko

Trivial: Oblicz √ i .

ICSP: √i = √0+i |z| = 1 y = 1 x = 0

	b
1 =
	0

wtf Popsułem coś Trzeba spróbować inaczej: 0+i |z| = 1

	π
q =
	2

n = 2

	q + 2kπ
√i = |z|(Ucos{q + 2kπ}{2} + isin		}
	2

	π		π		√2		√2
√i1 = (cos		+ i sin		) =		+ i
	4		4		2		2

	3π		3π		√2		√2
√i2 = (cos −		+ isin−		= −		− i
	4		4		2		2

Trivial: √ i = ? z = i = 0 + i. a = 0; b = 1; |z| = 1

	1
x = ±√12(a + |z|) = ±√12 = ±		.
	√2

	b		1
y =		= ... = ±		← nadużycie notacji ±, o której mówiłem wyżej.
	2x		√2

a więc:

	1+i
√ i = ±		.
	√2

ICSP: nie usunąłeś niewymierności z mianownika. Co jesli x = 0 ? Wtedy liczba zespolona nie istnieje czy jak?

Trivial: To może kolejne zadanie: z = |z|e^iφ. Wyprowadź wzór na logarytm o podstawie b z dowolnej liczby z. log_bz = ?

Trivial: Wiem, że nie usunąłem niewymierności, wyniki są takie same, ale √ i jest zwyczajowo podawany w takiej formie jak napisałem − z niewymiernością w mianowniku. Jeśli x = 0 to wróć do układu równań i zobacz co się dzieje... x nie może wyjść 0, chyba że liczysz trywialny pierwiastek z 0.

Trivial: Coś przeoczyłem. Jeśli x lub y = 0, to oznacza, że b = 0. A kto by liczył pierwiastek z liczby rzeczywistej wzorem zespolonym.

ICSP: Ja bym liczył z tym zadaniem z logarytmem to nie mam szans. Nawet nie wiem jak się za to zabrać.

Trivial: To zadanie z logarytmem jest dużo prostsze niż z pierwiastkiem. Podałem ci wskazówkę: z = |z|e^iφ

ICSP:

	z		z
z = |z|eiq ⇔ eiq =		⇔ lniq =		⇔ nie wiem
	|z|		|z|

Trivial: log_bz = log_b(|z|e^iφ) = ...

ICSP: = log_b |z| + iq log_b e. Da się to jeszcze bardziej uprościć?

Trivial:

	1
Tak, logbe =		← dla mnie prościej.
	lnb

ICSP: a to iq to co to jest? Ciągle to widuję ale jakoś nigdy się nie zastanawiałem co to oznacza.

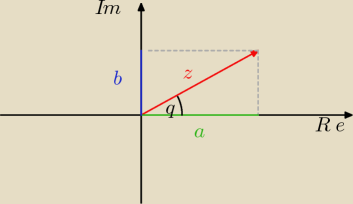
Trivial: q na rysunku oznacza φ. φ to argument liczby zespolonej (czyli po prostu kąt).

	b
sinφ =		→ b = |z|sinφ
	|z|

	a
cosφ =		→ a = |z|cosφ
	|z|

A więc... z = |z|cosφ + |z|sinφ*i = |z|(cosφ + isinφ). Można udowodnić, że e^iφ = cosφ + isinφ, a zatem: z = |z|e^iφ.

Trivial: Bierze się to z tego, że każdą liczbę zespoloną można przedstawić jako parę uporządkowaną (a,b), a zatem można zilustrować ją na płaszczyźnie zespolonej (taki 'układ współrzędnych' jak narysowałem wyżej). Re reprezentuje oś rzeczywistą, Im − urojoną.

ICSP: Czyli to tylko jest kąt? Czyli każdą liczbę zespoloną możemy zapisać za pomocą modułu i kąta?

Trivial: Tak.

ICSP: dobrze. To rozumiem. Następne zadanie

Trivial: Oblicz iⁱ.

ICSP: (0+i)ⁱ |z| = 1

	π
φ =
	2

0 + i = e^{i π/2} (e^{i π/2})ⁱ = e^{(i π/2)*i} = e^−π/2 Nie mam pomysłu na to.

Trivial: Policzyłeś. e^−π/2 Wynik jest rzeczywisty. Gratulacje. Btw, czy to nie dziwne, że coś tak urojonego jak iⁱ okazuje się być rzeczywiste?

ICSP: Trochę, ale rozwiązania trójmianu kwadratowego o współczynnikach rzeczywistych bywają zespolone.

ICSP: no dalej Muszę się troszkę podszkolić

Trivial: ICSP wiesz tyle ile trzeba. Ja miałem ze 2 wykłady z liczb zespolonych. W nadchodzącym semestrze będą bodajże funkcje zespolone i całki i różne takie.

ICSP: no to możesz dawać jakieś zadanka. Zobaczymy czy będę sobie dawał radę.

Trivial: Wyprowadź wzór:

	1
sinx =		(eix − e−ix)
	2i

i przy okazji:

	1
cosx =		(eix + eix)
	2

Powinno ci zająć trochę czasu. Ale jakoś specjalnie skomplikowane nie jest.

Trivial: LITERÓWKA.

	1
cosx =		(eix + e−ix)
	2

ICSP: e^ix = cosx + isinx e^−ix = cosx − isinx ( w potędze przed i jest minus to zapewne powinienem też postawić minus przed i przy sinusie. Jednak nie umiem tego udowodnić. e^−ix = cosx − isinx ⇔ cosx = e^−ix + isinx Teraz wstawiamy to do pierwszego równania: e^ix = cosx + isinx ⇔ e^ix = e^−ix + isinx+ isinx ⇔ 2isinx = e^ix − e^−ix ⇔ sinx =

	i
		(eix − e−ix)
	−2

// Teraz wyznaczymy z drugiego równania isinx e^−ix = cosx − isinx ⇔ isinx = cosx − e^−ix I wstawiamy to do pierwszego: e^ix = cosx + isinx ⇔ e^ix = cosx + cosx − e^−ix ⇔ 2cosx = e^ix + e^−ix ⇔ cosx =

	1
		(eix + e−ix)
	2

Trivial: e^−ix = e^i(−x) = cos(−x) + isin(−x) = cosx − isinx.

ICSP: to tak to działa Mógłbym na to nie wpaść Może popróbujmy równania kwadratowe.

Trivial: I można po prostu odjąć/dodać stronami.

ICSP: to daj przykład równania kwadratowego

Trivial: Rozwiąż równanie: z² − 2iz − 6 = 0.

ICSP: no to jedziemy z² − 2iz − 6 Δ = 4i² + 24 = 20 √Δ = 2√5 z₁ = 1 + √5 z₂ = 1 − √5 Trivial to jakiś żart z tym zadaniem był? To nawet licealista by zrobił

Trivial: To było zadanie na rozgrzewkę.

Trivial: Wyznacz pierwiastki równania: iz² + 5z − 9 = 0.

ICSP: Δ = 25 + 36i √Δ = √25 + 36i a = 25 , b = 36 , |z| = √1921 yyy coś pomyliłem?

Trivial: Liczby zupełnie losowe.

Trivial: Dobra zmieniamy iz² + z − 1 = 0.

ICSP: Δ = 1 + 4i √Δ = √1 + 4i a =1, b = 4 , |z| = √17 Nie możesz wymyślić jakiegoś równania gdzie moduł wyjdzie normalny? Weź jakieś trójkąty egipskie.

Trivial: iz² + √3z − 1 = 0.

ICSP: Δ = 3 + 4I √Δ = √3 + 4i a = 3 , b = 4 , |z| = 5 − trójkąt egpiski x = 2 y = 1 √Δ = 2+i

	√3 + 2 + i		−√3i − 2i +1
z1 =		=
	2i		2

	−√3i + 2i − 1
z2 =
	2

Trivial:

ICSP: no wreszcie Dasz normalne liczby i idzie. Przyznaję że jednak twój wzorek sie przydał

Trivial: Pytanie: dlaczego mogliśmy przyjąć za pierwiastek z delty akurat 2+i, a nie np. −(2+i)?

ICSP: ale to chyba bez różnicy.

Trivial: To bez różnicy, ale dlaczego?

ICSP: ponieważ później przy wstawianiu do pierwiastków jest to bez znaczenia. Możemy najpierw wstawić do pierwszego, albo do drugiego. To sprężenie licznika decyduje o tym.

Trivial: Masz ochotę na następne zadanko? Udowodnij, korzystając z liczb zespolonych, że: 2sinxcos3x = sin3x − sinx.

ICSP: nie rozumiem polecenia " korzystając z liczb zespolonych"

Trivial: Ze wzorów na sinusy i cosinusy, które wyprowadziłeś wyżej.

ICSP: a co zrobić jeśli mam sin2x?

Trivial: Idę sobie zrobić kakao. Jak wrócę ma być udowodnione!

ICSP: ale ja mam teraz film. Będę dopiero koło 22:30

Trivial: Wstawiasz w wykładnik zamiast x→2x

b.: to iⁱ nie jest dobrze zdefiniowane, trzeba by się umówić, że bierzemy argument z jakiegoś konkretnego przedziału np. i= e^iπ/2 −> dostanie się iⁱ = e^−π/2 i= e^5iπ/2 −> dostanie się iⁱ = e^−5π/2... nie ma tego problemu, jeśli podstawa jest dodatnia (co do tego, jak jest zdefiniowany logarytm z liczby dodatniej nie ma wątpliwości). Gdy nie, trzeba zaznaczyć, o jaką gałąź logarytmu chodzi (jak widać z powyższego, za ln(i) można przyjąć równie dobrze iπ/2, jaki i też 5iπ/2...)

Trivial: Tak. We wszystkich przykładach chodziło mi o argument główny, czyli z przedziału [0, 2π]. Dobrze, że o tym mówisz rozwiewając wątpliwości.

Trivial: z przedziału: [0, 2π) ! Wiadomo o co chodzi.

ICSP: 2sinxcos3x = sin3x − sin

	1		1		1
2		(eix − e−ix)*		(e3ix + e−3ix) =		(e3ix − e−3ix) −
	2i		2		2i

	1
		(eix − e−ix)
	2i

czy jest to samo co : (e^ix − e^−ix)* (e^3ix + e^−3ix) = (e^3ix − e^−3ix) − (e^ix − e^−ix) Przemnożyłem przed 2i oraz skróciłem 2 z 2?

Trivial: Trzeba wyjść z lewej strony, pomnożyć po kolei wyrazy i ma wyjść to co po prawej.

Trivial: Trzeba skorzystać z faktu, że: a^b*a^c = a^b+c...

ICSP: dzięki. Na razie pytałem się czy wszystko dobrze przekształciłem.

Trivial: Na razie jest OK.

ICSP: (e^ix − e^−ix)(e^3ix + e^−3ix) = e^4ix + e^−2ix − e^2ix − e^+4ix = e^−2ix − e^2ix Dobrze do tego momentu?

ICSP: omg. Nic nie mów. Bez tego ostatniego = . NIe śmiej się

Trivial: Widzę, że się skompromitowałem. Źle przepisałem. Trzeba pokazać, że 2sinxcos2x = sin3x − sinx. sorry.

ICSP: tyle pracy na nic. Jutro się tym zajmę Właśnie coś z tymi 4 mi nie pasowało. Dobranoc

Trivial: Ale masz dobrze. Możesz iść dalej i zobaczymy co wyjdzie. (bez ostatniego)

Trivial: Zresztą już wyszło co miało wyjść.

	1
... =		[e4ix − e−4ix − (e2ix − e−2ix)] = sin4x − sin2x.
	2i

Trivial: Ja też idę. Dobranoc.

ICSP: to jak? Uznajemy to zadanko jako zrobione? Jak tak to dawaj następne najlepiej z obliczaniem n−tej potęgi liczby zespolonej.

Trivial: Zadanka na n−tą potęgę liczby zespolonej są trudne do wymyślenia. Może jeszcze jedno trygonometryczne. Przy użyciu liczb zespolonych rozłóż na sumę sinusów wyrażenie: sin(x)cos(3x)cos(5x)

Trivial: Widzę, że coś słabo idzie.

b.: tak dla przestrogi dodam, że argument główny często jest definiowany jako argument z przedziału <−π, π)

ICSP: czasu nie miałem. Zabiorę się za to późnym wieczorem

Piotr student: Trivial proszony do mojego postu