trójkat
jj: W trójkącie prostokątnym ABC, C=90, poprowadzono wysokość CD. Wyznacz miary kątów ostrych w tym
trójkącie, wiedząc, że |AC|=|BD|−|AD|.
29 sie 11:00
ICSP: 90,60,30.
Zakładam że to C = 90 jest miarą kąta ACB a nie długością któregoś z boków.
29 sie 11:28
ICSP:
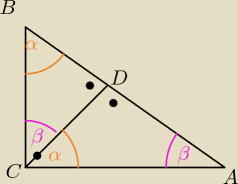
wiemy że : |CA| = |BD| − |AD| oraz że ∡ACB = 90
o
zapisujemy |AB| = |AD| + |BD| i z twierdzenia Pitagorasa liczymy:
|CB| =
√|AB|2 − |CA|2 = 2
√|AD||BD|.
|CD| =
√|AD|*|BD|
| | |CD| | | √|AD|*|BD| | | 1 | |
sinα = |
| = |
| = |
| ⇔ α = 30o oraz |
| | |CB| | | 2√|AD|*|BD| | | 2 | |
β = 60
o
29 sie 11:38
Gokx:
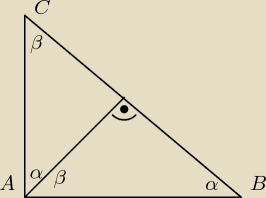
Mam pytanie czy tak zależność kątowa α i β występuje w kazdym trójkącie prostokątnym w którym
poprowadzimy wysokość

?
29 sie 11:59
ICSP: Jeżeli wysokość jest prowadzona z wierzchołka kąta prostego to tak.
29 sie 11:59
Gokx: dzieki

29 sie 12:00
 wiemy że : |CA| = |BD| − |AD| oraz że ∡ACB = 90o
zapisujemy |AB| = |AD| + |BD| i z twierdzenia Pitagorasa liczymy:
|CB| = √|AB|2 − |CA|2 = 2√|AD||BD|.
|CD| = √|AD|*|BD|
wiemy że : |CA| = |BD| − |AD| oraz że ∡ACB = 90o
zapisujemy |AB| = |AD| + |BD| i z twierdzenia Pitagorasa liczymy:
|CB| = √|AB|2 − |CA|2 = 2√|AD||BD|.
|CD| = √|AD|*|BD|
 Mam pytanie czy tak zależność kątowa α i β występuje w kazdym trójkącie prostokątnym w którym
poprowadzimy wysokość
Mam pytanie czy tak zależność kątowa α i β występuje w kazdym trójkącie prostokątnym w którym
poprowadzimy wysokość ?
?
