 Przeliczymy to analitycznie
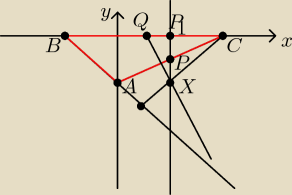
Przeliczymy to analitycznie  Połóżmy układ współrzędnych w taki sposób, aby BC leżało na osi
OX, a punkt A na osi OY pod osią OX, dodatkowo przyjmijmy taką jednostkę, aby A(0;−2),
przyjmujemy, że B(2bx , 0) , C(2cx , 0), oczywiście bx , cx ≠ 0 (jeżeli któreś by było
równe 0 to dostalibyśmy trójkąt prostokątny, który kąta rozwartego nie może mieć)
Punkt P ma wówczas współrzędne P(cx , −1), czyli P1(cx ; 0), skąd PP1 wyznacza prostą
x=cx. Punkt Q ma współrzędne Q(bx+cx , 0), prosta AC ma postać:
Połóżmy układ współrzędnych w taki sposób, aby BC leżało na osi
OX, a punkt A na osi OY pod osią OX, dodatkowo przyjmijmy taką jednostkę, aby A(0;−2),
przyjmujemy, że B(2bx , 0) , C(2cx , 0), oczywiście bx , cx ≠ 0 (jeżeli któreś by było
równe 0 to dostalibyśmy trójkąt prostokątny, który kąta rozwartego nie może mieć)
Punkt P ma wówczas współrzędne P(cx , −1), czyli P1(cx ; 0), skąd PP1 wyznacza prostą
x=cx. Punkt Q ma współrzędne Q(bx+cx , 0), prosta AC ma postać:
| x | ||
2cx(y+2) = 2x ⇔ y = | −2 | |
| cx |
| x | ||
2bx(y+2) = 2x ⇔ y = | −2, czyli prosta prostopadła do niej ma postać y = −bx*x+b, | |
| bx |
