Udowodnij, że dwusieczna dzieli kąt .... xyz: Udowodnij, że w trójkącie prostokątnym dwusieczna kąta prostego dzieli na połowy kąt zawarty między środkową, a wysokością opuszczoną z wierzchołka kąta prostego.

Eta: Godzio ...... do dzieła

Eta: ICSP ..... do dzieła

Jack: ciekawa własność... Zostawię to młodszym wyjadaczom

Godzio: Hmmm

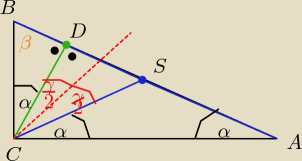
Eta: to może teraz................

Jack: no tylko bez podpowiedzi

Eta:

Eta: No co jest z Wami ....Godzio, ICSP

Eta: Chyba,że xyz już sobie teraz poradzi?

Godzio: Dlaczego tam jest trójkąt równoramienny ( ASC ) ?

Jack: okrąg opisany narysuj na ABC

Eta: Godzio ... nie osłabiaj mnie

Godzio: Może powiem wymigająco, że jestem padnięty po basenie więc niezbyt myślę

Eta:

Eta: A co na to "amator " ?

Godzio: Mam wakacje Nie robię zadań !

Jack: oo, dobra odpowiedź!

Eta: Dobre alibi

Eta: Każdy matematyk rozwiązuje zadania "w świątek, piątek i .... wakacje"

Eta: Tak jak.............. np; Trivial

Godzio: Oj tam, oj tam

Eta: No dobra, daruję CI ..... poczekamy na ICSP

rumpek:

	90o
Dwusieczna podzieliła kąt przy wierzchołku C na 2 więc:		= 45o
	2

	γ
Więc:		= 45o − α
	2

Wysokość pada na odcinek |AB| pod kątem prostym (nie widać za bardzo na rysunku). Z trójkąt prostokątnego w ΔABC mamy: β = 90^o − α (ponieważ odcinki |SA| oraz |CS| są to promienie opisanego okręgu na tym trójkącie prostokątnym, dlatego kąty α są równej długości) Chcąc wyznaczyć α przy odcinku |BC| (ten na przeciwko β) otrzymuje równość:

	γ
45o −		= 90o − β
	2

Wiem, że β = 90^o − α to teraz tylko podstawiam

	γ
45o −		= 90o − 90o + α
	2

	γ
45o −		= α
	2

	γ
45o −		− α = 0
	2

	γ
45o − α =
	2

	γ
No i chyba otrzymaliśmy tę równość bo tamten pierwszy		= 45o − α rozpatrywałem przy tym
	2

dolnym trójkącie równoramiennym. Znacznie łatwiej byłoby jakby były różne oznaczenia np.: γ i δ. Wtedy δ = 45^o − α(dolny), natomiast γ = 45^o − α (górny). Lub skorzystać z samych oznaczeń kątów Nie wiem czy dobrze czy nie niech sprawdzi fachowiec

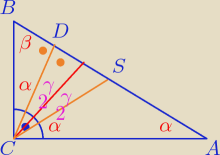
Gustlik: Trójkąt ASC jest równoramienny, ponieważ gdyby na trójkącie ABC opisano okrąg, to S byłby środkiem tego okręgu. Zatem |CS|=|SA|=R (promieniowi okręgu). Stąd równe kąty α przy podstawach trójkąta ASC. Trójkąt BCD jest podobny do ABC na mocy cechy kąt−kąt (wspólny kat β i kąt D=kątowi C=90^o), stąd kąt BCD=α. Wiemy, że dwusieczna dzieli kat na pół, zatem kąt prosty zostanie podzielony na dwa kąty po 45^o. Każdy z tych dwóch kątów zawiera kąt α i jest od niego większy o taki sam "kawałek", zatem kąty oznaczone przez Etę jako γ/2 muszą być równe. c.n.d.

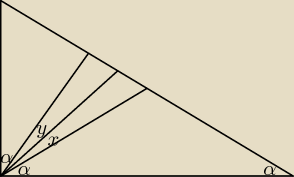
oj tam oj tam: α + x = 45 i α + y = 45 x = y

ICSP: już rozwiązane? Ja sobie nie poradzę z tym. Zbyt głupi jestem.

Jack:

xyz: Skąd wiemy, że kąt BCD=α?

xyz: ok już wiem BCD≈ABC.

xyz: Dzięki wszystkim jeszcze mam pytanie: jaki był poziom tego zadania ? na maturze podstawa czy rozszerzenie ?

Godzio: Studia

def: mówisz poważnie? Ja to znalazłem w lubelskie próbnej maturze dla klasy 1 poziom podstawowy ...

Godzio: Żartuje