 1.zad
Wykonaj działania (pamiętaj o założeniach ):
1.zad
Wykonaj działania (pamiętaj o założeniach ):
| x−1 | 3 | 1 | ||||
1) | − | + | ||||
| x | x2 | x+1 |
| 27 − x3 | 2x | |||
2) | * | |||
| 9+3x+x2 | 3−x |
| x2−1 | x2+7x+12 | |||
3) | * | |||
| x2+x−6 | x2+x−2 |
| 1 | 2 | |||
a) | − | =1 | ||
| x+2 | x−1 |
| 2x | x−4 | |||
b) | + | =1 | ||
| x+1 | x−1 |
| x+1 | x−2 | x2+x+12 | ||||
c) | + | = | ||||
| x−3 | x+1 | x2−2x−3 |
| 5−2x | ||
a) | ≤0 | |
| x−5 |
| −3x+4 | ||
b) | ≥−1 | |
| 4x+2 |
| 1 | 1 | |||
c) | ≤ | |||
| 2x−3 | 2x+8 |
| 3−2x2 | ||
d) | ≥−x | |
| 2x |
| 2x+4 | 1 | |||
e) | ≥ | |||
| 2x2−x−3 | x+1 |

 Zad 3
Zad 3
| 5 − 2x | ||
a) | ≤ 0 | |
| x − 5 |
| 5 | ||
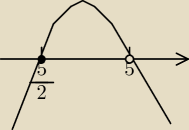
−2(x − | )(x − 5) ≤ 0 | |
| 2 |
| 5 | ||
x∊(−∞, | > U (5, +∞) | |
| 2 |
| −3x + 4 | ||
b) | ≥ − 1 | |
| 4x + 2 |
| −3x + 4 | −(4x + 2) | ||
≥ | |||
| 4x + 2 | 4x + 2 |
| −3x + 4 | 4x + 2 | ||
+ | ≥ 0 | ||
| 4x + 2 | 4x + 2 |
| x + 6 | |
≥ 0 | |
| 4x + 2 |
| 1 | ||
D = R − { − | } | |
| 2 |
| 1 | ||
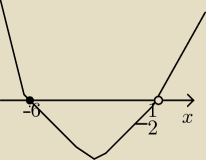
4(x + 6)(x + | ) ≥ 0 | |
| 2 |
| 1 | ||
x∊(−∞, −6>U(− | , +∞) | |
| 2 |
| x2−1 | x2+7x+12 | (x−1)*(x−4) | ||||
3)3) | * | = | ||||
| x2+x−6 | x2+x−2 | x−2 |
| (x−1)*(x−4) | ||
czy tak sama nie wiem eh  | ||
| (x−2)2 |
 bo to najważniejsze
bo to najważniejsze
| x − 1 | 3 | 1 | (x−1)x2 | 3x | 1 | ||||||
− | + | = | − | + | = | ||||||
| x | x2 | x+1 | x3 | x3 | x + 1 |
| x3 − x2 − 3x | 1 | |||
= | + | = | ||
| x3 | x + 1 |
| (x3 − x2 − 3x)(x + 1) | x3 | ||
+ | = ... | ||
| x3(x + 1) | x3(x + 1) |
 Raczej się nie pomyliłem xD Chociaż bardzo dawno to miałem i
mogłem zapomnieć xD
Raczej się nie pomyliłem xD Chociaż bardzo dawno to miałem i
mogłem zapomnieć xD
 mógłbyś mi to dokończyć może zrozumiem nareszcie to
A pozostałem 2 wyniki mam dobre ?
mógłbyś mi to dokończyć może zrozumiem nareszcie to
A pozostałem 2 wyniki mam dobre ?
| x4 − x3 − 3x2 + x3 − x2 − 3x + x3 | x4 + x3 − 4x2 − 3x | ||
= | |||
| x3(x + 1) | x3(x + 1) |
 !
No i chyba się nie pomyliłem
!
No i chyba się nie pomyliłem  xD Sprawdź bo mi się za bardzo nie chce
xD Sprawdź bo mi się za bardzo nie chce 

| 3 | ||
d) się zacięłam znowu w | ≥0 | |
| 2x |

| 1 | 1 | ||
≤ | |||
| 2x − 3 | 2x + 8 |
| 3 | ||
D = R − { | , −4} | |
| 2 |
| 2x + 8 | 2x − 3 | ||
≤ | |||
| (2x − 3)(2x + 8) | (2x − 3)(2x + 8) |
| 2x + 8 − (2x − 3) | |
≤ 0 | |
| (2x − 3)(2x + 8) |
| 11 | ||||||||||
≤ 0 | ||||||||||
|
| 3 | ||
22(x − | )(2x + 8) ≤ 0 | |
| 2 |
| 3 | ||
44(x − | )(x + 4) ≤ 0 | |
| 2 |
| 3 − 2x2 | |
≥ −x | |
| 2x |
| 3 − 2x2 | −2x2 | ||
≥ | |||
| 2x | 2x |
| 3 − 2x2 + 2x2 | |
≥ 0 | |
| 2x |
| 3 | |
≥ 0 | |
| 2x |
| 2x + 4 | 1 | ||
≥ | |||
| 2x2 − x − 3 | x + 1 |
| 1 − 5 | ||
x1 = | = −1 | |
| 4 |
| 1 + 5 | 6 | 3 | ||||
x2 = | = | = | ||||
| 4 | 4 | 2 |
| 3 | ||
D = R − {−1, | } | |
| 2 |
| 2x + 4 | 1 | |||||||||||
≥ | ||||||||||||
| x + 1 |
| 1 | 3 | |||
w e) jest x=−5 | x=−1 x= | |||
| 2 | 2 |
| 3 | ||
a w c) x=−4 i x= | ||
| 2 |
 w c już chyba wiesz co miałaś źle
w c już chyba wiesz co miałaś źle ?
?

| 2x + 4 |
| ||||||||||||||||||||
≥ | |||||||||||||||||||||
|
|
| ||||||||||
≥ 0 | ||||||||||
|
| ||||||||||||||||
≥ 0 | ||||||||||||||||
|
| ||||||||||
≥ 0 | ||||||||||
|
| 11 | 3 | |||
(x + | )(x + 1)(x − | ) ≥ 0 | ||
| 2 | 2 |
| 11 | 3 | |||
x∊<− | , −1) U ( | , +∞) | ||
| 2 | 2 |
 Tu masz rozwiązanie do e)
Tu masz rozwiązanie do e)