parametr majkaa: Wyznacz te wartości parametru m (m należy do R) dla których jeden z pierwiastków równania mx² − (2m+1)x+m−2=0 jest ujemny a drugi większy od 5.

rumpek:

⎧	m≠0
⎜	x1*x2 < 0
⎨	f(5)<0
⎩	Δ>0

Takie warunki powinny starczyć

majkaa: a mógłbyś to rozwiązać? proszę

rumpek: 1^o m nie może być 0 bo inaczej byłoby tylko jedno rozwiązanie 2^o Δ > 0 (dwa różne rozwiązania) Δ > 0 ⇔ (2m + 1) − 4*(m−2)*m = 4m² + 4m + 1 − (4m² − 8m) = 4m² + 4m + 1 − 4m² + 8m =

	1		1
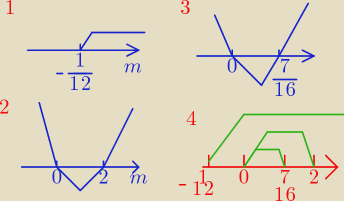
= 12m + 1 > 0 ⇒ 12m > − 1/ : 12 ⇒ m > −		(Rysunek 1) (x∊(−		, + ∞) )
	12		12

	c
3o x1x2 < 0 (Warunek na ujemny pierwiastek) x1x2 =
	a

m − 2
	< 0 ⇔ (nierówność wymierna) m(m−2) < 0 (Rysunek 2) ( x∊(0,2) )
m

4^o Warunek na tę 5. Podstawiamy za x 5 i mamy: ( Tutaj uwaga pomyliłem się powinno być: m*f(5) < 0 teraz jest corect ) m(25m − 5(2m + 1) + m − 2) < 0 m(25m − 10m − 5 + m − 2) < 0 m(16m − 7) < 0

	7		7
16m(m −		) < 0 (Rysunek 3) ( x∊(0,		) )
	16		16

To teraz jako punkt 5^o pozostało część wspólną dać Rysunek 4 Czyli odpowiedź to:

	7
x∊(0,		))
	16

Pozdrawiam

rumpek: Ten warunek: m*f(5) < 0 (poprawiony) gwarantuje to, że jak m jest ujemna i f(5) jest dodatnie lub gdy m jest dodatnie i f(5) jest ujemne

majkaa: dziękuje bardzo za szczegółowe wyjaśnienie