uzasadnij majkaa: wewnątrz trójkąta ABC wybrano dowolny punkt S. Uzasadnij że |kątCSB| > |kątCAB|

majkaa: proszę o pomoc

Jack: zobacz co się dzieje z kątami przy wierzchołkach B i C, gdy dorysujesz odcinki do punktu S (zauważ, że kąt B w obu trójkątach jest takich sam).

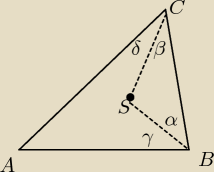
TPB: ∡BSC = 180⁰−α−β ∡BAC = 180⁰ − α−β−γ−δ ∡BSC−∡BAC = 180⁰−α−β−180⁰+α+β+γ+δ = γ+δ ∡BSC − ∡BAC = γ+δ>0 ⇒ ∡BSC−∡BAC >0 ⇔ ∡BSC>∡BAC c.b.d.o.

Jack: no tak, literówka: B i C się zmniejszają a A się nie zmienia... Niemniej masz już rozwiązanie.