pomóżcie
ania: W trójkącie ABC prowadzimy środkową CD. Udowodnij, że jeśli BC>AC to środkowa CD tworzy
większy kąt z bokiem AC niż z bokiem BC.
Jak to zrobić ze wskazówką: Narysuj półprosta CD i odłóż na niej odcinek DE (E≠C) taki, ze
|DE|=|CD|. Rozpatrz trójkąt EBC. Próbowałam wykazać że trójkąt ADC jest przystający do
trójkata EBC.
Proszę o rysunek.
26 sie 13:46
ania: pomoże ktoś?
26 sie 16:10
rumpek:
Jak narysowałaś rysunek to gites. Dobrze zaczęłaś bo trzeba wykazać praktycznie tylko
przystawanie trójkątów ADC oraz EBC. Jak już to zrobisz to zauważysz odpowiednio, że |BE| =
|AC|
oraz kąt ∡BED jest równy kątowi ∡ACD. No to wiemy jeszcze, że |BC| > |BE|. I na tym praktycznie
dowód się kończy bo naprzeciw dłuższego boku jest większy kąt czyli: ∡BED > ∡BCE
c.n.u.
Osobiście zrobiłem innym sposobem to zadanie (skorzystałem z sin i cos co wydaje się ciekawsze

)
26 sie 16:42
rumpek: Jakby co zajrzę na forum koło 23 teraz idę na jazdy, pa

26 sie 16:42
26 sie 17:00
TPB: rumpekowi chodziło o kąty ADC i BDE
27 sie 08:23
ania: przecież pisze o przystawaniu trójkątów
27 sie 11:49
ania: może ktoś to mi wyjaśnić?proszę
27 sie 14:36
rumpek:
Hmm

chyba zrobiłem zły rysunek sobie

ale teraz podam sposób który będzie poprawny na
100%

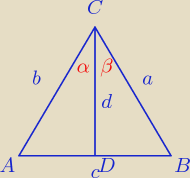
Rysunek powyżej
Skoro a > b to wiemy również, że α > β (naprzeciw dłuższego boku jest większy kąt)
Teraz przyrównamy pola ΔADC oraz ΔBDC
ΔBDC = U{adsinβ}
bsinα = asinβ
Wyznaczam a i otrzymuje:
Wiem, że a > b więc podstawiam:
bsinα > bsinβ
sinα > sinβ
Przy założeniu α,β∊(0
o, 90
o)

c.n.u.
27 sie 14:45
ania: a skąd wiesz że pola trójkątów ADC oraz BDC są równe?
27 sie 18:08
sushi_ gg6397228:
|AD|= |BD| i maja taka samą długosc wysokosci
27 sie 18:14
ania: nareszcie zrozumiałam.dzięki
27 sie 19:34
ania: a jak to zrobić tą poprzednią metodą?
28 sie 11:05
 )
)

 https://matematykaszkolna.pl/forum/kwadratPrzezroczysty.gif
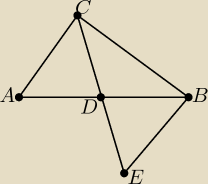
Jak tak robię rysunek to trójkąty ADC i EBC nie są przystające. Albo źle robię rysunek albo nie
widzę z której cechy skorzystać. Może trzeba wykazać przystawanie EBC i AEC
https://matematykaszkolna.pl/forum/kwadratPrzezroczysty.gif
Jak tak robię rysunek to trójkąty ADC i EBC nie są przystające. Albo źle robię rysunek albo nie
widzę z której cechy skorzystać. Może trzeba wykazać przystawanie EBC i AEC
 Hmm
Hmm  chyba zrobiłem zły rysunek sobie
chyba zrobiłem zły rysunek sobie  ale teraz podam sposób który będzie poprawny na
100%
ale teraz podam sposób który będzie poprawny na
100%  Rysunek powyżej
Skoro a > b to wiemy również, że α > β (naprzeciw dłuższego boku jest większy kąt)
Teraz przyrównamy pola ΔADC oraz ΔBDC
Rysunek powyżej
Skoro a > b to wiemy również, że α > β (naprzeciw dłuższego boku jest większy kąt)
Teraz przyrównamy pola ΔADC oraz ΔBDC
 c.n.u.
c.n.u.