Sławek: W półkole o promieniu R wpisano prostokąt o największym polu. Obliczyć cosinus kąta rozwartego między przekątnymi tego prostokąta.

0: a to jest ciekawe ...

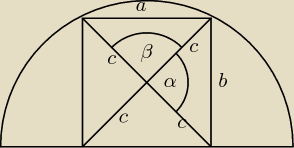
pomagacz: jeśli chodzi o prostokąt o największym polu, to chodzi na pewno o kwadrat

	c		c
cos(α) = cos(β) =		=
	b		a

c		c
	=
b		a

ac = cb a = b α = 90^o cos(90^o) = 0

Sławek: kwadrat to chyba zbyt banale

pomagacz: a jaką masz odpowiedź?

Sławek: Może i kwadrat, tylko to trzeba wykazać, a Ty od tego zacząłeś. Ja to nazywam metodą odwrotnego przekształcania odpowiedzi.

Zofia: To tak, jakby powiedzieć: kwadrat jest kwadratowy, bo jest kwadratem

Sławek:

a
	= cosβ
R

0,5b
	= sinβ
R

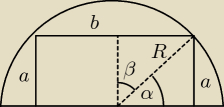
P = ab = Rcosβ * 2Rsinβ = 2R² sinβcosβ = R² sin2β P'(β) = R² * 2cos2β P'(β) = 0 ⇔ R² * (−2sin2β) = 0 ⇔ sin2β=0 ⇔ 2β = 0 (odrzucamy bo wtedy nie będzie prostokąta) lub 2β = 90^o cos2β = cos90^o = 0

anubas: wydaje mi się, że liczycie cosinus złego kąta, przecież pytanie jest o cosinus pomiędzy przekątnymi tego prostokąta, a jego boki wynoszą 1/2r√2 i r√2, to nie jest kwadrat

anubas: poprawna odpowiedź to −3/5