 Z oczywistych powodów, xśm = zśm = 0.
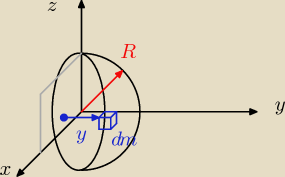
Parametryzacja kuli:
x = rcosφcosθ
Z oczywistych powodów, xśm = zśm = 0.
Parametryzacja kuli:
x = rcosφcosθ
| π | π | |||
Φ: y = rsinφcosθ (r, φ, θ)∊[0, R]×[0, π]×[− | , | ] | ||
| 2 | 2 |
| ∫ydm | ||
yśm = | ||
| m |
| m | m | 3m | ||||||||||||||||
ρ = | = | = | . | |||||||||||||||
| V |
| 2πR3 |
| R4 | cos2θ+1 | ρR4 | sin2θ | |||||
= ρ* | *(−cosπ + cos0)*∫ | dθ = | *[ | +θ] = | ||||
| 4 | 2 | 4 | 2 |
| ρπR4 | 3m | πR4 | 3 | |||||
= | = | * | = | mR. | ||||
| 4 | 2πR3 | 4 | 8 |
| ∫ydm | 3 | |||
yśm = | = | R. | ||
| m | 8 |
