pomocy ania: W trójkącie ABC prowadzimy środkową CD. Udowodnij, że jeśli |CD| > 1/2|AB| to miara kąta przy wierzchołku C jest mniejsza od 90 stopni.

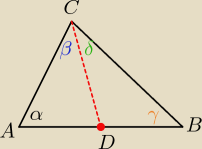
Eta: |∡<C|= β +δ naprzeciw najdłuższego boku leży kąt o największej mierze w ΔADC: jeżeli |CD|> |AD| ⇒ α > β w ΔDBC: jeżeli |CD|> |DB| ⇒ γ > δ dodając te nierówności stronami otrzymujemy: 2|CD| > |AD|+ |DB| ⇒ α + γ> β+δ 2|CD |> |AB| ⇒ α+γ> |∡<C|

	1
|CD| >		|AB} ⇒α+γ+|∡<C|> 2 |∡<C| i α+β+|∡C|= 180o
	2

to: 180^o > 2|∡C| /:2 |∡C|< 90^o c.n.u

ania: dzięki

Teothor: |∡<C|= β +δ naprzeciw najdłuższego boku leży kąt o największej mierze w ΔADC: jeżeli |CD|> |AD| ⇒ α > β w ΔDBC: jeżeli |CD|> |DB| ⇒ γ > δ dodając te nierówności stronami otrzymujemy: 2|CD| > |AD|+ |DB| ⇒ α + γ> β+δ 2|CD |> |AB| ⇒ α+γ> |∡<C| 1 |CD| > |AB} ⇒α+γ+|∡<C|> 2 |∡<C| i α+γ+|∡C|= 180o 2 to: 180o > 2|∡C| /:2 |∡C|< 90o c.n.u mały błąd . zamiast β ma byc γ

niewiem: jak dokładnie postępujecie w momencie gdzy dzielicie nierówność przez 2?, tzn nie wiem skąd się bierze α+γ+|C|> 2|C|