Sławek: Wykaż, że jeżeli kąty trójkąta spełniają warunek sinγ =2cosα sinβ, to trójkąt jest równoramienny.

rumpek: Twierdzenie sinusów i cosinusów i zadanko rozwiązane

rumpek: Zaraz się za nie biorę

Sławek: oki

losek: α + β + γ = 180^o, γ = 180^o − (α + β), sinγ = sin(α + β) = sinαcosβ + sinβcosα sinαcosβ + sinβcosα = 2sinβcosα sinαcosβ − sinβcosα = 0 sin(α − β) = 0 α − β = 0^o α = β

Godzio: Chyba to jest wystarczający dowód, aczkolwiek mogę się mylić sinγ = sin(α + β) = sinαcosβ + cosαsinβ = 2cosαsinβ sinαcosβ − cosαsinβ = 0 sin(α − β) = 0 ⇒ α − β = 0 ⇒ α = β

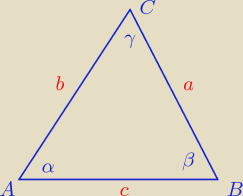
rumpek: Tak jak pisałem wyżej z tw. sinusów:

	a
1o		= 2R
	sinα

	b
2o		= 2R
	sinβ

	c
3o		= 2R
	cosγ

1^o

a
	= 2R / * sinα
sinα

a = 2R * sinα / : 2R

	a
sinα =
	2R

2^o

b
	= 2R / * sinβ
sinβ

b = 2R * sinβ / : 2R

	b
sinβ =
	2R

3^o

c
	= 2R / * sinγ
sinγ

c = 2R * sinγ / : 2R

	c
sinγ =
	2R

Twierdzenie cosiunusów (wystarczy jak wyznaczymy tylko kąt cosα − więc do roboty) a² = b² + c² − 2bccosα 2bccosα = b² + c² − a² / : bc

	b2 + c2 − a2
2cosα =		(dwójki nie usuwam bo będę wykorzystywał tezę i będzie łatwiej)
	bc

Więc masz tam podane: sinγ = 2cosαsinβ Podstawiamy:

c		b2 + c2 − a2		b
	=		*		/ * 2R
2R		bc		2R

	b2 + c2 − a2
c =		* b / : b
	bc

c		b2 + c2 − a2
	=		/ * bc
b		bc

c² = b² + c² − a² c² − c² = b² − a² b² = a² ⇒ b = a c.n.u. Kiedyś się nauczyłem tej metody i tak ją wykorzystuje wiem, że można łatwiej tak jak Godzio czy losek

Sławek: chyba tak , bo w trójkącie równoramiennym kąty przy podstawie są sobie równe.