
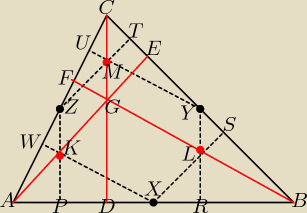

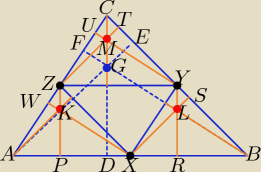
 Warto zauważyć, że środki boków trójkąta: X, Y i Z są wierzchołkami trójkątów przystających:
AXZ, XBY, ZYC i XYZ. Ortocentra trzech pierwszych trójkątów przecinają się w punktach:
K, L, M. Trzeba wykazać, że te ortocentra leżą na wysokościach trójkąta ABC, który jest
podobny do tych trzech trójkątów (AXZ, XBY, ZYC) w skali 2:1.
Warto zauważyć, że środki boków trójkąta: X, Y i Z są wierzchołkami trójkątów przystających:
AXZ, XBY, ZYC i XYZ. Ortocentra trzech pierwszych trójkątów przecinają się w punktach:
K, L, M. Trzeba wykazać, że te ortocentra leżą na wysokościach trójkąta ABC, który jest
podobny do tych trzech trójkątów (AXZ, XBY, ZYC) w skali 2:1.

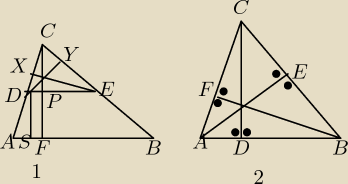 a) D,E są odpowiednio środkami boków AC i BC, skąd wynika, że AB || DE, trójkąty ABC i DEC są
podobne, czyli wysokość CF w trójkącie ABC pokrywa się z wysokością CP w trójkącie DEC, więc
aby pokazać, że DY , EX , CF przecinają się w jednym punkcie wystarczy pokazać, że DY , EX ,
CP przecinają się w 1 punkcie, co jest równoważne pokazaniu, że wysokości w dowolnym trójkącie
przecinają się w jednym punkcie. Teraz z 2 rysunku widzimy, że z wierzchołka F widać AB pod
tym samym kątem co z wierzchołka E, skąd na czworokącie ABEF da się opisać okrąg, niech to
będzie okrąg o1, analogicznie na BCFD da się opisać okrąg o2 oraz na CADE da się opisać
okrąg o3. Zauważmy teraz, że oś potęgową okręgów o1 i o2 wyznacza wysokość BF, podobnie
osie potęgowe o2, o3 oraz o1 , o3 wyznaczają pozostałe wysokości. Osie potęgowe 3 okręgów
których środki nie są współliniowe są współpękowe, cnd. Analogicznie dowodzimy, że pozostałe
odcinki przecinają się na pozostałych wysokościach.
a) D,E są odpowiednio środkami boków AC i BC, skąd wynika, że AB || DE, trójkąty ABC i DEC są
podobne, czyli wysokość CF w trójkącie ABC pokrywa się z wysokością CP w trójkącie DEC, więc
aby pokazać, że DY , EX , CF przecinają się w jednym punkcie wystarczy pokazać, że DY , EX ,
CP przecinają się w 1 punkcie, co jest równoważne pokazaniu, że wysokości w dowolnym trójkącie
przecinają się w jednym punkcie. Teraz z 2 rysunku widzimy, że z wierzchołka F widać AB pod
tym samym kątem co z wierzchołka E, skąd na czworokącie ABEF da się opisać okrąg, niech to
będzie okrąg o1, analogicznie na BCFD da się opisać okrąg o2 oraz na CADE da się opisać
okrąg o3. Zauważmy teraz, że oś potęgową okręgów o1 i o2 wyznacza wysokość BF, podobnie
osie potęgowe o2, o3 oraz o1 , o3 wyznaczają pozostałe wysokości. Osie potęgowe 3 okręgów
których środki nie są współliniowe są współpękowe, cnd. Analogicznie dowodzimy, że pozostałe
odcinki przecinają się na pozostałych wysokościach.
| 1 | ||
b) Wynika to bezpośrednio z tego, że AB || DE, to, że |DS| = | |CF| wynika bezpośrednio z | |
| 2 |
| |AD| | 1 | |||
podobieństwa trójkątów ASD i AFC, które są podobne w skali k = | = | , | ||
| |AC| | 2 |