Geometria, udowodnij TPB: Dany jest trójkąt ostrokątny ABC. Obrano punkty D,E,F odpowiednio na bokach BC, CA i AB w ten sposób, że ∡ADB jest prosty oraz ∡EDA=∡FDA. Udowodnij, że AD, BE i CF przecinają się w jednym punkcie. Wydaje mi się, że te odcinki AD,BE i CF są wysokościami trójkąta ABC. W takim razie zadanie sprowadza się do pokazania, że trójkąty BCF oraz KDC (gdzie K to punkt przecięcia CF z AD) są podobne. Analogicznie dowodzimy dla drugiej pary trójkątów. Kiedy uzyskami, że są podobne, to możemy wywnioskować, że podane odcinki są wysokościami zatem przecinają się w jednym punkcie. Ale nic, a nic nie potrafię udowodnić tego podobieństwa. Proszę o rozwiązanie albo porządne wskazówki. No chyba, że rozwiązanie idzie jakoś inaczej, a moje przeczucie jest błędne.

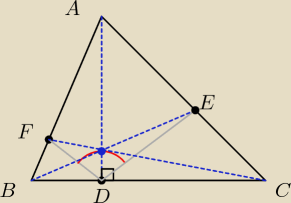
Trivial: Nie są wysokościami, bo możesz dowolnie wybrać punkt E, a linie i tak się przetną. Przynajmniej na rysunku. Myślę nad dowodem.

TPB: Racja! Kurcze a ja tyle błądziłem

Trivial: Może wyjść z twierdzenia Cevy, o którym sam pisałeś?

TPB: Z pewnością tak. Zadanie jest również podobne do tego od Vaxa. też trzeba wykazać, ze przecinają się w jednym punkcie. A do tego pomocne jest tw. Cevy

Godzio: Tak myślę, nie dało by się pokazać, że FC i EB są dwusiecznymi kątów DFE i DEF ?

TPB: Też miałem taki pomysł, ale jednak porzuciłem to, bo nic mi z tego nie wyszło. Nie wiem może wam się uda, bo mnie zadanie ciut przerasta, albo humor dzisiejszy nie pomaga mi w rozwiązywaniu geometrii

Trivial: Udowodniłem. Korzystając z twierdzenia Cevy, twierdzenia sinusów i prostych własności kątów.

TPB: Gratuluję Pochwal się, proszę

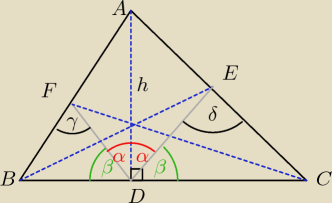
Trivial: Twierdzenie Cevy (odwrotne również OK):

	AF		BD		CE
Teza:		*		*		= 1
	AE		BF		CD

Najpierw zauważamy, że kąty β na rysunku są takie same. Teraz stosujemy 4 razy twierdzenie sinusów:

BD		BF		BD		sinγ
	=		→		=
sinγ		sinβ		BF		sinβ

CD		CE		CE		sinβ
	=		→		=
sinδ		sinβ		CD		sinδ

AF		h		hsinα
	=		→ AF =
sinα		sin(180o−γ)		sinγ

AE		h		hsinα
	=		→ AE =
sinα		sin(180o−δ)		sinδ

AF		sinδ
	=
AE		sinγ

AF		BD		CE		sinδ		sinγ		sinβ
	*		*		=		*		*		= 1 − O.K.
AE		BF		CD		sinγ		sinβ		sinδ

TPB: Elegancko