Oblicz prawdopodobieństwo zdarzenia A▯B. Aleksandra: Jak to obliczyć: P (A ∪ B) = P (A) + P (B) − P (A ∩ B) = gdy: P (A) = ¹₄ P (B) = ⁵₁₂ Wie może ktoś olśniony jak to obliczyć i poprawnie po podstawiać?

sushi_ gg6397228: brakuje jeszcze tekstu do zadania, tam za pewne jest ukryta bardzo pomocna informacja do rozwiazania tego zadania

pomagacz:

	1		5		3		5		8
P(A) + P(B) =		+		=		+		=
	4		12		12		12		12

P(A) + P(B) > 1 prawdopodobieństwa są zbieżne (nachodzą na siebie) ⇒ P(A ∩ B) istnieje P(A) + P(B) ≤ 1 prawdopodobieństwa nie są zbieżne (nie nachodzą na siebie) ⇒ P(A ∩ B) nie istnieje

pomagacz: sushi pewnie chodzi o niezależność prawdopodobieństwa

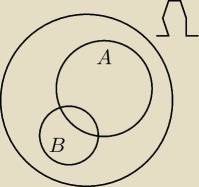
xXx: pomagacz to co napisałeś to jest bzdura wg ciebie jeśli P(A) + P(B) ≤ 1 to P(A∩B) nie istnieje a co powiesz o takiej sytuacji jak na rysunku?

Aleksandra: MOI KOCHANI! TEKST ZADANIA: Zad.1 Rzucono dwiema sześciennymi kostkami do gry i określono zdarzenia: A − na każdej kostce wypadła nieparzysta liczba oczek, B − suma wyrzuconych oczek jest nie mniejsza niż 8. Oblicz prawdopodobieństwo zdarzenia A▯B.

roman: @@ Pomagacz możesz mi coś wytłumaczyć mianowicie P(A)+P(B)>1

	8
przecież sam obliczyłeś że jest to		a to chyba < 1
	12

roman: dobra ja bym zrobił tak Ω= 36 P(A)= {1,3,5} P(B)= 1+3+5=9 >8 nie wiem czy db to zrobiłem [ zacząłem ] mógłby mnie ktoś sprawdzić >?

roman: up

sławek: Jakieś durnoty wypisuje tu roman, przecież prawdopodobieństwo jest liczbą należącą do przedziału <0, 1>

roman: to też mówię że by mnie ktoś poprawił ,,,

sławek: Nie znając wartości P(A∩B) nie można obliczyć P(A∪B). |Ω| = 36

	9
A − na każdej kostce wypadła nieparzysta liczba oczek, P(A) =
	36

	15
B − suma wyrzuconych oczek jest nie mniejsza niż 8, P(B) =
	36

A∩B − na każdej kostce wypadła nieparzysta liczba oczek i suma wyrzuconych oczek

	3
jest nie mniejsza niż 8, A∩B = {(3, 5), (5, 3), (5, 5)}, P(A∩B) =
	36

	9		15		3		21		7
P(A∪B) =		+		−		=		=
	36		36		36		36		12