Równanie, graniastosłup i walec. PILNE ! MARTI: Zadanie 1 Rozwiąż równanie:

x−2
	=−4
6x+3

Zadanie 2 Oblicz pole powierzchni graniastosłupa prawidłowego trójkątnego o krawędzi podstawy równej 3 i wysokości 4. Zadanie 3 Oblicz pole powierzchni i objętość walca w którym przekątna przekroju osiowego ma długość 8 i jest nachylona do płaszczyzny podstawy pod kątem 30 stopni.

dero2005: zad 2

	a2√3		32√3		9
Pp =		=		=		√3 − pole podstawy
	4		4		4

P_s = a*h = 3*4 = 12 − pole ściany

	9
Pc = 2*Pp + 3*Ps =		√3 + 36 − pole powierzchni całkowitej
	2

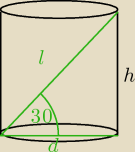
dero2005: zad 3 l = 8

d		√3
	= cos 30o =
l		2

	l√3
d=		= 4√3 − średnica
	2

h
	= sin 30o = 12
l

	l
h =		= 4 − wysokość
	2

	πd2
Pp =		= 12π − pole podstawy
	4

V = P_p*h = 12π*4 = 48π − objętość P_b = πd*h = 4π√3*4 = 16π√3 − pole powierzchni bocznej P_c = 2*P_p + P_b = 2*12π + 16π√3 = π(24 + 16√3) − pole powierzchni calkowitej

Eta:

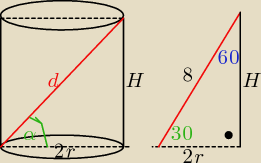
	1
1/ założenie 6x+3≠0 <=> x≠ −
	2

(6x+2)*(−4)=x−2 dokpończ............ 2/ P_c=2P_p+P_b a=3, H=4 P_p=a²√3}{4}=.......... P_b=3*a*H=..... P_c=...... 3/ H=4 , d = 8 2r=4√3 to r=2√3 V=πr²*H=.............. P_c=2πr²*H+2πrH=......... dokończ obliczenia

Eta: i ot ........... dero już Cię wyręczył w rachunkach

dero2005: zad 1

x−2
	= −4
6x+3

D 6x+3 ≠ 0 x ≠ −¹₂ x−2 = −4(6x+3} x − 2 = −24x − 12 25 x = −10 5x = −2 x = −²₅