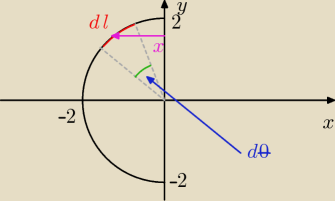
 Z powodu symetrii oczywiste jest, że yśm = 0.
Z powodu symetrii oczywiste jest, że yśm = 0.
| ∫xdm | ||
xśm = | ||
| m |
| m | m | |||
λ = | = | . | ||
| L | πR |
| m | ||
dm = λdl = λRdθ = | dθ | |
| π |
| R | ||||||||||||
xśm = | = | ∫cosθdθ | |||||||||||
| m | π |
| π | 3π | |||
Ustalamy granice całkowania: | ≤ θ ≤ | . | ||
| 2 | 2 |
| 3π | π | |||
∫π23π2 cosθdθ = sin | − sin | = −2. | ||
| 2 | 2 |
| 2R | ||
xśm = − | . | |
| π |
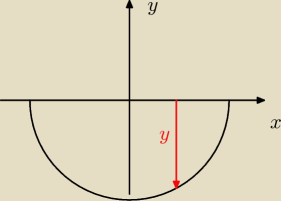 Z tym że jest zły rysunek... Dla twojego zadania powinien być taki... Możesz rozwiązać
analogicznie dla y = Rsinθ, stwierdzając, że xśm = 0.
Z tym że jest zły rysunek... Dla twojego zadania powinien być taki... Możesz rozwiązać
analogicznie dla y = Rsinθ, stwierdzając, że xśm = 0.
| 2R | ||
Powinno ci wyjść to samo, czyli yśm = − | . | |
| π |