zadanie otwarte z matury poprawkowej 2011 koko: Kąt α jest ostry i sin α = 1/4 Oblicz 3+2 tg²α. Zrobiłem to tak narysowałem przykładowy trójkąt prostokątny i oznaczyłem boki: tgα= ¹_x x²+1²=4² x²= 16−1 x²=15 x=√15 tgα= ¹_√15 * ^√15_√15 = ^√15₁₅ podstawiłem: 3+2 (^√15₁₅)² 3+2 ¹⁵₂₂₅ po skróceniu: 3+ 2¹_√15 = 3²₁₅ Czy rozwiązałem je poprawnie. Proszę o opinię

koko: oczywiście po skróceniu 3+ 2 ¹₁₅ bez pierwiastka na dole

ICSP:

	1
sinα =
	4

	√15
cos α =
	4

	1		4		1
tgα =		*		⇔ tg2α =
	4		√15		15

	1		1
3 + 2		= 5
	15		15

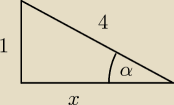
pomagacz: tak

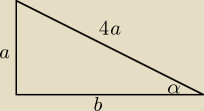
maturek: b = √16a² − a² = a√15,

	a		a		1
tgα =		=		=
	b		a√15		√15

	1		2
3 + 2tg2α = 3 + 2*		= 3
	15		15

maturek: Nie można przyjmować długości 1 i 4, bo znamy tylko stosunek tych liczb. Mogą przecież być długości 2 i 8 albo 3 i 12. Trzeba przyjąć a i 4a (literka nie ma znaczenia, może być k i 4k)

ICSP:

	1		2
3 + 2		= 3		. Nie wiem co mi się w głowie poprzewracało wcześniej głupoty
	15		15

powypisywałem.

koko: Czy moja wersja rozwiązania jest poprawna? dostanę chociaż punkt

Basia: możemy maturku, bo wszystkie trójkąty z przyprostokątną a i przeciwprostokątną 4a są podobne mają więc kąty o tych samych miarach możemy więc sobie wybrać jeden z nich; na przykład ten z 1 i 4 albo, jak kto woli, ten z 5 i 20

Basia: dostaniesz koko maksymalną liczbę punktów, Twoje rozwiązanie jest całkowicie poprawne

Ela: Czy jeżeli zrobiłam do tego momentu: tgα= 1 przez √15 dostanę jeden punkt? Zapomniałam usunąć niewymierność... *ściana*

maturek: Niestety Basiu, nie możemy, formalność zapisu tego zadania wymaga zapisania długości boków przy znajomości tylko ich stosunku w postaci takiej, jak podałem.

Basia: Nieprawda. Mogę sobie wybrać jeden z trójkątów podobnych spełniających warunki zadania. Oczywiście rozwiązanie ogólne jest o wiele bardziej eleganckie, ale nie bezwzględnie konieczne. Rozumiem, że zęby Ci zgrzytają. mnie też jeszcze dwa, trzy lata temu zgrzytały, ale już się przyzwyczaiłam. Można to zresztą uzasadnić: trójkąt a,4a,a√15 ∼ trójkąta 1,4,√15 ⇒ miary kątów trójkąta (1) = miarom kątów trójkata (2) ⇒ funkcje trygonometryczne liczone w każdym z tych trójkątów są takie same ⇒ mogę liczyć na bazie jednego konkretnego. I na bazie tego uzasadnienia tak uczą w szkołach. I CKE to akceptuje.

Gustlik: Maturku, niestety Basia ma rację. W dodatku czytałem w jakimś dokumencie z CKE opublikowanym w internecie, chyba to był raport z zeszłorocznej matury, ze można tak rozwiązywać, jak podają Basia i Pomagacz. Komisja musi uznać takie zadanie jako poprawne. Oczywiście Twój sposób też jest dobry, jest bardziej ogólny. Twoim sposobem mozna byłoby rozwiązywać takie zadanie, w którym byłoby polecenie, żeby oprócz funkcji obliczyć coś jeszcze, np. boki trójkąta, ale wtedy musiałaby być podana jakaś informacja, z której dałoby się obliczyć a. Ale przy obliczaniu samych funkcji trygonometrycznych to a nie jest potrzebne, wynika to z podobieństwa trójkątów. Pozdrawiam