ARKUSZ MATURALNY POPRAWKOWY Marta..: ZRÓBCIE ZADANIA MATURALNE kto umie oczywiscie....bo odpowiedzi nigdzie jeszcze nie znalazlam ..... http://www.mmtrojmiasto.pl/photo/1130337/Matura+poprawkowa+2011+-+Odpowiedzi%2C+arkusze%2C+rozwi%C4%85zanie+zada%C5%84#photoBrowsing

xXx: 1 3(2−3x)=x−4⇔6−9x=x−4⇔10x=10⇔x=1

Marta..: dobrze.jesli umiesz inne to zrob je po kolei

xXx: 2

	15x
x+		=230
	100

xXx: 3 {x+3y= 5 ⇒ x=5−3y {2x−y=3 2(5−3y)−y=3 ⇔ 10−6y−y=3⇔ −7y=−7⇔y=1 y=1 ⇒ x=5−3=2

xXx: 4 dla f(x)=ax+b f(x)↗ ⇔ a>0 m−2>0 ⇔ m>2

xXx: 5 {2=a+b⇒ b =2−a {5=−2a+b 5=−2a+2−a ⇔ −3a=3 ⇔ a= −1 a= − 1 ⇒ b=2−a=3 f(x) = x+3

xXx: 6 k: y=ax+b, k ⊥ y=x+1 ⇒ a= − 1 A=(0,5) ∊ k ⇒ 5=0+b ⇒ b=5 k: y= −x + 5

xXx: 7 {a²−b²=200 ⇒ (a+b)(a−b)=200 {a+b=8 (a−b)=200/8=25

xXx: 8 |5−2|+|1−6|=3+5=8

xXx: 9 log₂4 + 2log₃1 = 2 + 0 =2

xXx: 10 dla f(x)=x²−4 D⁻¹ = <−4;∞)

xXx: 11 deg W(x) = 3 deg V(x) = 3 więc ich różnica to 0

xXx: 12

	15
q=		=3
	5

a₅=a₄q=15*3=45

xXx: 13 1001 1100 1010 2000 więc są 4 takie liczby

xXx: 14 |AB|=√(2−1)² − (3+4)² = √1 + 49 = √50 = 5√2

pomagacz: Odpowiedzi do tych zadań na razie, bo system się przepełnił: 1. A 2. C 3. A 4. A 5. D 6. B 7. A 8. A 9. D 10. A 11. B 12. D 13. D 14. C 15. D 16. C 17. C

xXx: 15 sin(90−α) = cosα cos47^o=sin(90^o−47^o)=sin43^o

Marta..: oki..dziekuje

xXx: 16 2n²−9 < 0 ⇔ 2n² < 9 n∊ ℤ ⇒ n∊{−2, −1, 0, 1, 2}

rupert: W pierwszym zadaniu otwartym Δ=1, x₁=1, x₂=2

rupert: A dalej nie wiem, bo strona się wysypała.

xXx: 17 d=√9²+(9√2)²=9√3

Marta..: ale jakie nawiasy w tym wlasnie trzeba bylo napisac....otwarte czy zamkniete?

xXx: 18 _

	3+1+1+0+x+2
x = 2 =		⇒ x = 5
	6

xXx: 19 |Ω|=90 A={30, 60, 90} ⇒ |A|=3

	3
P(A)=
	90

xXx: 20 V=π*3²*6=54π

rupert: a>0, Δ>0 czyli ramiona paraboli skierowane w górę

rupert: 1<x<2

xXx: 21

	√3
P=42sin60o=16*
	2

Marta..: nie oto chodzi..chodzi jak zapisac przedział...? czy tak : 1. (1,2) czy tak 2. <1,2>?

K. : 17) 9√3? Na pewno? W innych rozwiązaniach jest inaczej i zdycham tu z nerwów

rupert: nawiasy oczywiście otwarte

xXx:

	4
V=288π =		πr3 ⇒ r3=216 ⇒ r=6
	3

Marta..: a ja zaznaczyłam zamkniete nawiasy i co myslisz ze dadzą mi chociaż z 1 punkt?

xXx: w 17 na pewno 9√3

xXx: Ostatnie zamknięte : 23 9a=90 ⇔ a=10

	a2√3
Pc =		* 2 + 3a2 = 50√3+300
	4

anecia851: a w zadaniu 2 ? jaka odp? 0.5*x=230 ? czy inna bo nie wiem

Marta..: ok.. teraz otwarte

anecia851: nie rozumiem odp. w 16 zadaniu

Marta..: w zadaniu drugim : x + 0,15x = 230

Marta..: w 16 zadaniu masz zamiast N wstawic liczbe...np 1 i obliczac... i wynik ma byc ujemny..

xXx: w 16 zadaniu: 2 liczby ujemne

Marta..: xXx: MASZ ŹLE W 16.. za N po prostu wstawia sie liczby.....1 i 2 tylko pasuja.. bo maja byc ujemne..

Marta..: a no tak 2 liczby

:): Pisaliscie poprawke? jak wam poszło jaki poziom?

xXx: w 11 pomyłeczka należało odjąć najpierw te wielomiany a więc stopień nowopowstałego to 1 czyli B

:): Pisaliscie poprawke? jak wam poszło jaki poziom?

Marta..: poziom hm mozliwy, ten kto sie uczył napewno zda..ale otwarte moim zdaniem byly nie lekkie...i to niby poprawka..

Godzio: Kolega mówił, że banalne, gdyby się pouczył to by zdał

Marta..: no wlasnie w 11 tez to zauwazylam, ale dobrze ze juz sprostowales innym

:): aha..spoko Marta a czemu niby poprawka ma być łatwiejsza/

xXx: z tego co rozwiązałem to banał, na arkuszu same zamknięte się dało zrobić w pół godziny obstawiam

:): Każdy mając mature z tego roku musi mieć podobny poziom obojetnie czy zdaje w 1 terminie cyz poprawce, a nie jedni pisaliby poziom sredni a drudzy niski? bezsens

Marta..: bo to poprawka.a ogólnie to moim zdaniem na te 30% powinno sie dawac b.proste zadania. bo niektózy nie chca wiazac przyszlosci z matematyka

Godzio: A poprawka rozszerzonego też będzie ? Bo coś podobnego było chyba rok temu

Marta..: ale to tylko moja oopinia..wiec nikogo nie osądzam..

Marta..: ale mi chodzi o to ze ogólnie własnie POWININEN BYC TAKI SAM POZIOM.ale na te 30% powinny byc typowe..a w szkole u mnie np. polowy zadań nie widziałam.............dopiero jak przeanalizowałam arkusze to coś mi się tam rozjasniło..

Marta..: a ktos zrobi 26? otwarte

xXx: 25 16 ∏ = 2¹*3*2²*5*2¹*3*7*2³*9*2¹*5*11*2²*3*13*2¹*7*15*2⁴ = X * 2¹⁵ k=1 a więc iloczyn ten jest podzielny przez 2¹⁵

life: no wlasnie jestem ciekawa otwartych. w 26. wyszlo mi ⁴⁷₁₅ ale pewnie zle

pomagacz: 1. 3(2 − 3x) = x − 4 6 − 9x − x + 4 = 0 −10x = −10 x = 1 2. x + 15%x = 230 1% = 0,01 x + 0,15x = 230 3.

⎧	x + 3y = 5
⎩	2x − y = 3 \\ * 3

⎧	x + 3y = 5
⎩	6x − 3y = 9	[+]

−−−−−−−−−−−−−−− 7x = 14 x = 2 2 + 3y = 5 3y = 3 y = 1

⎧	x = 2
⎩	y = 1

4. f(x) = (m − 2)x − 11 f(x)↗ dla a > 0 m − 2 > 0 m > 2 5. A = (1, 2) B = (−2, 5)

⎧	2 = a + b ⇒ a = 2 − b
⎩	5 = −2a + b

5 = −2(a − b) + b 5 = −4 + 2b + b 9 = 3b b = 3 2 = a + 3

⎧	a = −1
⎩	b = 3

6. A = (0, 5) k ⊥ y = x + 1 g = a_gx + b a_g = −a b = y_A = 5 k = −x + 5 7. a² − b² = 200 a + b = 8 (a + b)(a − b) = 200

	200
a − b =
	a + b

	200
a − b =
	8

a − b = 25 8. |5 − 2| = |3| = 3 |1 − 6| = |−5| = 5 |5 − 2| + |1 − 6| = 3 + 5 = 8 9. log_ab ⇒ x^a = b, a > 0 log₂4 ⇒ x² = 4 x² = 4 x = ±2 x = 2 2log₃1 ⇒ x³ = 1 x³ = 1 x = 1 10. f(x) = x² − 4 D⁻¹: a > 0, (b, +∞) a < 0, (−∞, b) a > 0 D⁻¹: <−4, +∞) 11. W(x) = x³ + 3x² + x − 11 V(x) = x³ + 3x² + 1 W(x) − V(x) = x³ + 3x² + x − 11 − (x³ + 3x² + 1) = x³ + 3x² + x − 11 − x³ − 3x² − 1 = x − 12 12. a₃ = 3 a₄ = 15

	a4		15
q =		=		= 3
	a3		5

a₅ = a₄ * q = 15 * 3 = 45 13. 1001 1010 1100 2000 14. A = (1, −4) B = (2, 3) |AB| = √(x_B − x_A)² + (y_B − y_A)² = √(2 − 1)² + (3 + 4)² = √1 + 49 = √50 = 5√2 15. sin(α) = cos(47^o) cos(47^o) = sin(90^o − 47^o) = sin(43^o) 16. a_n = 2n² − 9, n ≥ 1 a₁ = 2 − 9 = −7 a₂ = 8 − 9 = −1 a₃ = 18 − 9 = 9 17. |\ 9 | \ x | \ −−−− 9√2 9² + (9√2)² = x² 81 + 81 * 2 = x² 243 = x² x = 9√3

:): heh pewnie było tylko Ty tak uważałas, te zadania są tak banalne wszystkie ze szkoda gadac,ja też nie wiąże swojej kariery z polskim bo jestem na politechnice ,ale jakieś wiadomości trzeba mieś,czy z polskiego czy historii czy z wszytskich innych przedmiotow, a nie byc tłumokiem ze srednim wyksztalceniem,

Marta..: life mi tez tak wyszlo ⁴⁷₁₅

Marta..: moze masz racje ...ale tez nie kazdy ma umysł ścisły..niektórzy nie maja zdolnosci do maatematyki.. naszczescie nie mowie o sobie

:): no ja tez nei mam zdolnosci do pisania wypracowac i pamieci do wsyztskich przedmiotow humanistycznych ,ale niestety wazne zeby chciec

xXx:

	47
dobry wynik		w 26
	15

Marta..: no w sumie tak, ale wiesZ? zawsze sa za i przeciw..

Marta..: uff! super ze wyszedl wyniki ⁴⁷₁₅

Humanistka: Dzięki za rozwiązania! Uważam że było nieco łatwiej niż na maturze majowej, na pewno w przypadku zamkniętych. Jeżeli te wyniki tutaj są poprawne to zdałam. ZDAŁAM. Nemezis mojego życia, matematyka, pokonana... Płaczę ze szczęścia. Idę poczytać książki czego nie mogłam robić cały sierpień przez babranie się w cyferkach. Peace out.

Marta..: to ile w końcu wyszlo w 21 zadaniu?

:): no pewnie niedługo "scisłowcy" beda strajkowac ,ze nie chcą polskiego na maturze,tak na powaznie to najlepsze wyjscie to pisanie ze wszystkich przedmiotow takiego testu nawet w ramach szkoły a nie ogolnopolskiej matury i byłby spokoj kazdy musiałby umiec chociaz podstawy danego przedmiotu

life: po skroceniu 8√3, chyba

xXx: tak 8√3

:): +wtedy jak kiedys powrot do testow wstępnych na uczelnie wyzsze i tyle

Marta..: −−− > moze masz i racje..ale narazie jest matura wiec dopóki zmiany nastapia to minie spooro czasu.na szczescie mnie juz one nie beda dotyczyc.oczywiscie mam nadzieje ze zdalam tą maturkę dzisiejsza..odbiore świadectwo maturalne ii git

Marta..: a no fakt w 21 macie racje 8√3... pomylilam sie

:): " ...ale tez nie kazdy ma umysł ścisły..niektórzy nie maja zdolnosci do maatematyki.. naszczescie nie mowie o sobie"−czyli jednak masz problemy z mattematyką

:): w sumie i tak możecie się dostać pewnie gdzie chcecie jest niż więc miejsc na studiach jeszcze sporo

Marta..: no bo sie nie uczylam do matury.. a teraz poduczylam sie i zdalam z tego co patrzylam teraz na odpowiedzi lenistwo mnie odwiedzilo hehe w maju. i wczesniej...

Marta..: tak wlasnie dostane wyniki 15.09. i wlasnie do tego dnia moge sobie pojechac i zlozyc bo sa wolne miejsca na uczelniach..

Marta..: a jak trzeba zrobic 28?

Marta..: i 32?

life: wynika maja byc 13

Marta..: a u nas mowili ze 15..to moze innne okręgi czy cos.. nie wiem....ale dziekuje ze powiedzialas/es

Marta..: a w 27 zadaniu mi jakims dziwnym trafem wyszlo −1/6 .. i nie wiem czemu ale no coż 2 pkty mniej

sandikay: A w przed ostatnim zadaniu , jakie było równanie? To było o tym boisku jak coś

Marta..: ja juz normlanie ide bo mam dosc tej matmy jak na 1 dzien za duzo jej

sandikay: Dwie szkoły mają prostokątne boisko. Przekątna boiska jest równa 65m. Boisko w drugiej szkole ma długośc o 4m wieksza niz boisko w pierwszej szkole, ale szerokość o 8m mniejsza. Oblicz długosc i szerokosc kazdego z tych boisk. Jakie jest równanie? x+y = 65 (x+4) (y−8) = 65

Eta: x−−−dł.boiska pierwszego y −−−szerokość pierwszego, x,y>0 x+4 −−− dł drugiego y−4 −−− szer. drugiego x²+y²=65² (x+4)²+(y−8)²=65² x²+8x+16+y²−16y+64=x²+y² x=2y−10 (2y−10)²+y²=65² y²−8y−825=0 Δ=3364, √Δ=58 y=33 lub y= −25 −−−− odrzucamy to: x= 2y−10 x= 56 1 boisko ma wymiary 56m −−−−długość , 33m −−− szerokość 2 boisko ma wymiary: 60m −−− długość , 25m −−− szerokość

sandikay: Oki , dziękuję Ja niestety nie pomyślałam o tym ze ma być 65²

rumpek: Wie ktoś może czy matura poprawka z rozszerzonej tak jak rok temu była ?

Pestek: no własnie wie ktoś?

całeczki: a kto CI powiedział ze rok temu była poprawa roz?

Pestek: https://matematykaszkolna.pl/strona/matura.html sierpień 2010 poziom roz i pod jest.

całeczki: ni ebyło czegoś takiego chyba sobie jaja robicie

Adek: mam pytanie. Pisałem poprawkę z matmy i tam było zadanie z boiskami za 5pkt. Czy za wypisanie danych dostanę 1pkt. Bardzo proszę o odpowiedź.

Kici ;): chyba tak, ale nie jestem pewna Ale nie martw się Adek na pewno zaliczyłeś

Kici ;): a matematyka rozszerzonej to moim zdaniem nie ma poprawki, tylko z matmy pod. bo jest obowiązkowa, a dodatkowe przedmioty to już nie da się poprawić, chyba że w następnym roku się napiszę jeszcze raz. do całeczki

Renata: To może jeszcze za samo przeczytanie treści zadania należy się punkt? Punkty przyznaje się za rozwiązanie, a nie za przepisanie danych

Kici ;): Ale chyba są za to punkty, tak słyszałam xD

iga: A zad, 28 ktoś może pokazać, jak to miało być? (ten dowód geometryczny) I jeszcze, jaki wynik ma być w zad. 30 (te 2 pudełka)?

iga: Może jeszcze zad.32 ktoś pokazać? B. proszę.

iga:

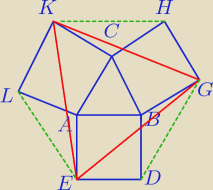
rumpek: Zadanie 28 Wiadomości podstawowe: − trójkąt równoboczny (wszystkie boki równe oraz kąty po 60^o ) − kwadrat (wszystkie boki równe [nie widać za bardzo tego na moim rysunku ale żyjemy xD] i kąty po 90^o) Zadanie rozwiążemy na podstawie przystawania trójkątów. Trójkąt KGE (ten co mamy go wykazać oznaczyłem czerwonymi kreskami ) 1^o Rozpatrujemy kąt ∡DBG (ma on 360^o − 90^o − 90^o − 60^o = 120^o) 2^o Rozpatrujemy kąt ∡EAL (podobnie jak w/w kąt ma 120^o ) 3^o Znowu rozpatrujemy kolejny kąt ∡HCK (również ma 120^o) Zajmijmy się teraz trójkątem BGD jest on równoramienny ( |BD| = |BG| ) Rozpatrzmy teraz trójkąt EAL jest on również równoramienny ( |AL| = |AE| ) Ostatni trójkąt rozpatrujemy: CHK także równoramienny bo ( |CH| = |CK| ) Teraz zauważamy, że wszystkie te trójkąty (ΔBGD i ΔEAL oraz ΔHCK ) są przystające na podstawie (b,k,b). Odpowiednie boki są równe |BD| = |BG| = |AL| = |AE| = |CH| = |CK| a także mają równe kąty: ∡DBG = ∡EAL = ∡HCK = 120^o. Czyli wiemy, że (przerywane odcinki zielone są równe |DG| = |EL| = |KH| ) To teraz patrzymy na przystawanie trójkątów : ΔEDG i Δ KLE oraz ΔKHG. Są one przystające bo mają równe boki: 1^o |HG| = |ED| = |KL| 2^o |KH| = |EL| = |DG| 3^o Odpowiednie kąty są równe ∡EDG = ∡ELK = ∡KHG (ale to już sama pomyśl dlaczego ) No to skoro wiemy, że wyżej wymienione trójkąty są przystające wiemy, że boki |KG| oraz |EG| oraz |KE| są równe więc jest to trójkąt równoboczny

rumpek: Zad. 30 Dane: − 10 kul w pudełku niebieskim − 10 kul w pudełku czerwonym Z reguły mnożenia obliczam moc |Ω| = 10* 10 = 100 |A| = 9 + 8 + 7 + 6 + 5 + 4 + 3 + 2 + 1 = 45 Z prawdopodobieństwa:

	|A|		45		9
P(A) =		=		=
	|Ω|		100		20

rumpek: Zadanie 32: Wpierw zapiszmy tę liczbę: − − − − − Pięciocyfrowa, zastanówmy się nad liczbami: możemy obsadzić z przedziału {0,1,2,3,4,5,6,7,8,9} Jednak tutaj 9 wywalamy (patrz punkt 4) ) Więc maksymalnie 9 liczb możemy wykorzystać na jedno miejsce. Zastanówmy się nad jednym (cyfry jedności [te na końcu], cyfry dziesiątek [przed ostatnie], cyfry setek [te na trzecim miejscu (−) kresce ] Więc pierwszą liczbę mogę wybrać na 8 sposobów (0 nie wchodzi w grę − inaczej nie była by 5−cyfrowa) Drugą liczbę mogę wybrać na 9 sposobów (0 już mogę wybrać) To teraz najtrudniejsza część zadania: Zastanówmy się nad pierwszym warunkiem (trzy ostatnie cyfry są parzyste więc mamy: 0,2,4,6,8) No i teraz najzwyczajniej w życiu szukamy takiego ułożenia: 1^o −−864 2^o −−862 3^o −−860 4^o −−842 5^o −−840 6^o −−820 7^o −−642 8^o −−640 9^o −−620 10^o −−420 No to mamy takich dziesięć przypadków więc otrzymujemy na podstawie reguły mnożenia: 8*9*10 = 720 Żebym taką maturkę w maju dostał No może bez tego dowodu

iga: Wielkie dzięki, rumpek. A to zad. 32 mozesz mi jeszcze pokazać?

:): Rumpek spokojnie, na samej maturze spinasz sie na maxa, sytuacja to warunkuje, wiec jak ogarniasz, a widze ze ogarniasz to spokojnie osiagniesz ≥96%

iga: O, już zrobiłeś. Śliczne dzięki. Pozdrawiam.

iga: I to zad. 28 było tylko za 2 punkty! Mało, uważam.

rumpek: Dowody zawsze na maturce podstawowej są na 2 pkt.

iga: Wiem, ale przyznasz, że ten dowód zasługiwał na więcej punktów.

rumpek: Niom, we wtorek 10 minut nad nim siedziałem dopiero potem skręciłem z przystawaniem co nie wydawało się trudne Dla mnie na maturce najgorsze będą dowody − dlatego teraz ich dużo rozwiązuje Przyda się na pewno ta wiedza.

iga: No na pewno się przyda. A gdzie się wybierasz?

iga: To Ty jeszcze nie zdawałeś matury? Myślałam, że już zdawałeś w tym roku.

rumpek: Za rok niestety w tym podstawa była łatwa Rozszerzenie muszę sie douczyć a tak to planuje iść na Uniwerek Wrocławski − Informatyka a ty? (w tym roku maturka / za rok? )

sandikay: Ja Was wszystkich podziwiam, tych którzy rozumieją matematykę i ją lubią. Na serio , dla mnie zdobycie 15pkt na maturze podstawowej jest wielkim wyczynem , chociaż wiem że niby to nie jest DUŻO. Pisałam w sierpniu poprawkę i boje sie że braknie mi 1pkt ... W zadaniu o tym boisku , napisalam równanie tak jak ktoś powyżej rozwiązał ale nie napisałam tego do kwadratu , także boje sie ze moge pożegnać się chociaż z 1pkt No ale jakoś trzeba dac rade pozdrawiam !