Oblicz pole trójkąta ABC, jeśli :
King James: A=(−3,−1) B=(−1,2) C= (1,−2) Proszę także o przebieg obliczeń ponieważ nie mam pojęcia, w
ogóle jak to zrobić. Z góry dziękuję!
23 sie 00:25
Gustlik: A=(−3,−1) B=(−1,2) C= (1,−2)
Skorzystam ze wzoru wektorowego − NAJPROSTSZY SPOSÓB:
gdzie d(AB
→, AC
→) − wyznacznik wektorów AB
→ i AC
→.
Wyjaśnienie tej metody tutaj:
https://matematykaszkolna.pl/forum/forum.py?komentarzdo=i18
Liczę współrzedne tych wektorów:
AB
→=B−A=[−1−(−3), 2−(−1)]=[2, 3]
AC
→=C−A=[1−(−3), −2−(−1)]=[4, −1]
Liczę wyznacznik wektorów:
d(AB
→, AC
→)=
| 2 3 |
| 4 −1 |
=2*(−1)−3*4=−2−12=−14 (mnożę na krzyż − pierwsza przekątna minus druga przekątna)
Odp. P=7
23 sie 00:54
Lelo: W sumie można też zastosować ciekawy wzorek...
| | 1 | |
P = |
| *|(Xb − Xa)(Yc − Ya) − (Yb − Ya)(Xc − Xa)| |
| | 2 | |
| | 1 | |
P = |
| *|(−1 − (−3))(−2 − (−1)) − (2 − (−1))(1 − (−3)) = |
| | 2 | |
| | 1 | | 1 | |
= |
| *|(−1 + 3)(−2 + 1) − (2 + 1)(1 + 3)| = |
| |2 * (−1) − 3 * 4| = |
| | 2 | | 2 | |
| | 1 | | 1 | | 1 | |
= |
| *|−2 − 12| = |
| * |−14| = |
| * 14 = 7 |
| | 2 | | 2 | | 2 | |
23 sie 12:22
Lelo: Zawsze możemy to też zrobić tak...
Liczę długość odcinka |AB|, będzie to również długość podstawy trójkąta...
|AB| =
√(Xb − Xa)2 + (Yb − Ya)2
A=(−3,−1) B=(−1,2)
|AB| =
√[−1 − (−3)]2 + [2 − (−1)]2 =
√(−1 + 3)2 + (2 + 1)2 =
√22 + 32 =
√13
Teraz wyznaczam równanie prostej AB i zapisuję je w postaci ogólnej...
(X
b − X
a)(y − Y
a) = (Y
b − Y
a)(x − X
a)
[−1 − (−3)][y − (−1] = [2 − (−1)][x − (−3)]
(−1 + 3)(y + 1) = (2 + 1)(x + 3)
2(y + 1) = 3(x + 3)
2y + 2 = 3x + 9
2y = 3x + 9 − 2
2y = 3x + 7/:2
Teraz korzystam ze wzoru na odległość punktu od prostej. Liczę odległość punktu C od prostej
AB, która jest jednocześnie wysokością trójkąta opadającą na podstawę AB.
| | |Ax0 + By0 + C| | |
d = |
| |
| | √A2 + B2 | |
| | 3 | | 7 | |
− |
| x + y − |
| = 0 C= (1,−2) |
| | 2 | | 2 | |
| | | | 3 | | 7 | | |− |
| * 1 + 1 * (−2) + (− |
| )| | | | 2 | | 2 | |
| |
d = |
| = |
| | | |
| | |−2 − 5| | | 7 | | 2 | | 14 | |
= |
| = |
| = 7 * |
| = |
| = |
| | | | | | √13 | | √13 | |
Mając długość podstawy i wysokości mogę obliczyć pole trójkąta korzystając z podstawowego
wzoru na jego pole...
| | 1 | | 1 | | 14√13 | |
P = |
| * a * h = |
| * √13 * |
| = |
| | 2 | | 2 | | 13 | |
| | 1 | | 14*13 | | 1 | |
= |
| * |
| = |
| * 14 = 7 |
| | 2 | | 13 | | 2 | |
23 sie 14:01
King James: Dzięki bardzo !
23 sie 14:41
Gustlik: Lelo, nie, żebym krytykował te metody, ale zauważ, że ten Twój "ciekawy wzorek" wziął się
z wyznacznika wektorów, czyli z "mojej" metody. Tylko ten "ciekawy wzorek" jest mniej strawny
od wektorowego, a na pewno trudniejszy do zapamietania.
Drugi spsób − dobry, ale "do Rzymu przez Krym".
Twoje metody są dobre, ale skomplikowane i nieprzejrzyste dla uczniów.
Pozdrawiam

23 sie 19:30
Lelo: Nie ma problemu. Tyle, że ja pisałem maturkę w tym roku

A matematyki na poważnie zacząłem
się uczyć w 3 liceum

Więc jak się chce, to się wszystko da

23 sie 23:06
bart:
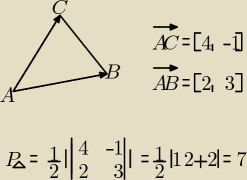
23 sie 23:37
Basia:
Gustlik wytłumacz może najpierw
Kingowi Jamesowi co to jest wektor, jak się liczy
jego współrzędne, jakie są prawa działań na wektorach i skąd się wziął wzór na pole, czyli po
kolei:
teraz jak w układzie współrzędnych policzyć sinus i cosinus kąta między wektorami (tu potrzebne
tw.sinusów i cosinusów)
jak już delikwent to wszystko zrozumie będzie mógł z tego skądinnąd bardzo przydatnego wzoru
skorzystać
ale zacznij od tego
co to jest wektor, po kolega zapewne z podstawy i nie ma o tym
pojęcia
a dla tych, którzy o wektorach nie słyszeli i nawet nie wiedzą co to za stwór, metoda
Lelo
jest niestety jedyną możliwą do pojęcia, chociaż nie przeczę, że strasznie żmudna i sama jej
serdecznie nie znoszę
24 sie 00:01
krystek: A może by tak jeszcze jeden sposób z wzoru Herona .Obl długość każdego boku (mniejsza możliwośc
popełnienia błędu) i mamy Pole .
Gustlik −pozwól ,że zwróce Tobie uwagę −nie wszyscy są błyskotliwi −nie ujmując nikomu tutaj na
forum. A jedyna słuszna droga żle mi sie kojarzy ,A Ty taka metodę stosujesz ,strofując
wszystkich którzy maja inne podejście do zadania .Czy barta zapis ,który jest czytelny też
zanegujesz?
24 sie 00:10
Gustlik: Krystek bart zrobił tą samą metodą, co ja − obliczył za pomocą wyznacznika wektorów.
Basiu − ja podałem link do strony z wyjaśnieniem metody. W dodatku w jednym z wątków
wyjaśniam tę metodę jeszcze raz za pomoca iloczynu wektorowego, można wyszukać wyszukiwarką.
Jeszcze jedno: skoro obecnie bez dowodów podaje się w szkole wiele wzorów, czego za "moich"
czasów nie było, to dlaczego nie można podać wzoru wektorowego, który jest prosty jak
konstrukcja cepa

? Co do wektorów ja już nie raz pisałem, jak liczy się ich współrzędne, po
to piszę: AB
→=B−A, co oznacz, że od współrzędnych punktu B trzeba odjąć współrzędne punktu A.
Wszystko to jest wina tego debila do n−tej potęgi z MEN−u, który ułożył taki program, że
wyciął większość potrzebnych wzorów i twierdzeń. Zreszta po to piszę o wektorach, żeby
zachęcić uczniów do sięgnięcia, choćby nawet na tej stronie, po ten materiał z rozszerzeń,
który powinien być na podstawie.
A propos − czytałaś
Basiu "mój" program? Tylko nauka wg tego programu gwarantuje sukces na
maturze PODSTAWOWEJ, bo nauka wg oficjalnego programu to jazda po wyboistych, nieoznakowanych
polnych dróżkach, gdzie łatwo jest zbłądzić. Taką polną dróżką są m.in. te metody obliczania
pola trójkata zaprezentowane przez
Lelo, a zwłaszcza ta druga, choć ten pierwszy wzór też
długi i mało przejrzysty, można się pomylić przy wstawianiu współrzędnych. Dlatego nie polecam
okrężnych metod, trzeba sie uczyć metod prostych, nawet jeżeli musimy sięgnąć do programu
rozszerzonego, bo tak naprawdę to na rozszerzeniach robi się zadania prościej niż na
podstawach − tak "madrze" skonstruowano program.
24 sie 01:53
krystek: Gustlik ,ależ oczywiście ,Barta zapisał to prosto,któtko i zwiężle ilustrując. Kiedyś ,kiedys
za moich czasów pradawnych było tak zapisywane,ale wówczas warunek równoleglości i
prostopadłości,kąt między wektorami był w programie.
.A jestem przeciwnikiem pisania wzorów podstawowych bez zrozumienia.
Nie obraź się ,ale jestes młody gniewny− nie narzucaj wszystkim swojego zdania.
Pamiętaj ,że są uczniowie przeciętni i wybitni −PATRZ→ VAX
.
24 sie 09:29
Gustlik: Ja niestety mam problemy z rysowaniem na tej stronie, jak chcę coś narysować, to mi kompa
zawiesza nie wiem czemu. Dlatego więcej piszę, bo chcę opisem "zobrazować" metodę. Ponadto ja
zachecam do zapoznania się z rachunkiem wektorowym, bo jest on prosty jak konstrukcja cepa i z
niezrozumiałych względów został usunięty z poziomu podstawowego. Ja swoich uczniów uczę
"starym" programem i dzięki temu rozumieją lepiej matmę.
Poza tym matematyka jest trochę pod względem metodyki jak prawo. Stara rzymska zasada głosi:
"ignorantia iuris nocet" co oznacza "nieznajomość prawa szkodzi". I podobnie w matematyce
"NIEZNAJOMOŚĆ METOD SZKODZI". Dotyczy to również metod z poziomu rozszerzonego, które
często ułatwiają rozwiązanie zadania z podstaw. Uważam, że lepiej jest raz wyprowadzić i
pokazać prosty wzór, a potem go stosować, zwłaszcza, że zadania z matematyki są powtarzalne, a
więc wyprowadzenie prostego wzoruczęsto jest po prostu opłacalne nawet czasowo, niż robić te
kilkanaście takich samych zadań metodami "do Rzymu przez Krym", które rozumie co dziesiąty
uczeń. Ja się nagadam, zleci cała lekcja, a uczeń jak nie umiał, tak nie umie, bo się myli w
obliczeniach. I materiał nie przerobiony, jak należy, bo czasu za mało. To wygląda tak, jakby
dać kierowcy godzinę czasu na przejazd z Warszawy do Piaseczna i kazać mu jechać przez
Szczecin. Nie wyrobi się, chyba żeby wynajął samolot.
24 sie 23:55
loll: loool
5 wrz 19:27

 A matematyki na poważnie zacząłem
się uczyć w 3 liceum
A matematyki na poważnie zacząłem
się uczyć w 3 liceum  Więc jak się chce, to się wszystko da
Więc jak się chce, to się wszystko da 
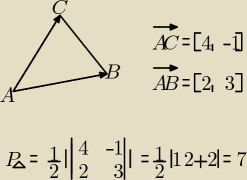
 ? Co do wektorów ja już nie raz pisałem, jak liczy się ich współrzędne, po
to piszę: AB→=B−A, co oznacz, że od współrzędnych punktu B trzeba odjąć współrzędne punktu A.
Wszystko to jest wina tego debila do n−tej potęgi z MEN−u, który ułożył taki program, że
wyciął większość potrzebnych wzorów i twierdzeń. Zreszta po to piszę o wektorach, żeby
zachęcić uczniów do sięgnięcia, choćby nawet na tej stronie, po ten materiał z rozszerzeń,
który powinien być na podstawie.
A propos − czytałaś Basiu "mój" program? Tylko nauka wg tego programu gwarantuje sukces na
maturze PODSTAWOWEJ, bo nauka wg oficjalnego programu to jazda po wyboistych, nieoznakowanych
polnych dróżkach, gdzie łatwo jest zbłądzić. Taką polną dróżką są m.in. te metody obliczania
pola trójkata zaprezentowane przez Lelo, a zwłaszcza ta druga, choć ten pierwszy wzór też
długi i mało przejrzysty, można się pomylić przy wstawianiu współrzędnych. Dlatego nie polecam
okrężnych metod, trzeba sie uczyć metod prostych, nawet jeżeli musimy sięgnąć do programu
rozszerzonego, bo tak naprawdę to na rozszerzeniach robi się zadania prościej niż na
podstawach − tak "madrze" skonstruowano program.
? Co do wektorów ja już nie raz pisałem, jak liczy się ich współrzędne, po
to piszę: AB→=B−A, co oznacz, że od współrzędnych punktu B trzeba odjąć współrzędne punktu A.
Wszystko to jest wina tego debila do n−tej potęgi z MEN−u, który ułożył taki program, że
wyciął większość potrzebnych wzorów i twierdzeń. Zreszta po to piszę o wektorach, żeby
zachęcić uczniów do sięgnięcia, choćby nawet na tej stronie, po ten materiał z rozszerzeń,
który powinien być na podstawie.
A propos − czytałaś Basiu "mój" program? Tylko nauka wg tego programu gwarantuje sukces na
maturze PODSTAWOWEJ, bo nauka wg oficjalnego programu to jazda po wyboistych, nieoznakowanych
polnych dróżkach, gdzie łatwo jest zbłądzić. Taką polną dróżką są m.in. te metody obliczania
pola trójkata zaprezentowane przez Lelo, a zwłaszcza ta druga, choć ten pierwszy wzór też
długi i mało przejrzysty, można się pomylić przy wstawianiu współrzędnych. Dlatego nie polecam
okrężnych metod, trzeba sie uczyć metod prostych, nawet jeżeli musimy sięgnąć do programu
rozszerzonego, bo tak naprawdę to na rozszerzeniach robi się zadania prościej niż na
podstawach − tak "madrze" skonstruowano program.