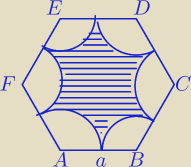
Pole zacieniowanej figyry Mila: Dla licealistów. 1) Wielokąt ABCDEF jest sześciokątem foremnym i jego obwód jest równy 36. Każdy wierzchołek sześciokąta jest środkiem okręgu o promieniu równym poło− wie długości boku. Ile jest równy obwód i pole zacieniowanej figury?

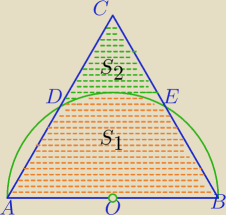
Mila: 2) W trójkącie równobocznym o boku długości 12 środek O boku AB jest jedno− cześnie środkiem koła o promieniu 6. Oblicz pola i obwody zakreskowanych figur S₁ i S₂

chichi: Widzę, że chcesz rozgrzać uczniów w tym nowym roku szkolnym, rzecz w tym, że to nie oni te zadania rozwiązują. Na maturę podstawową za 2pkt. w sam raz

Mila: To zadania z poziomu dawnych GM. Zgodnie z zasadą stopniowania trudności. Łatwe − potem trudniejsze. Ty już wrzuciłeś trudniejsze. I dobrze. Może będą rozwiązywali, jeśli damy im szansę.

chichi: @Mila czekam aż zacznie się wysyp zadań domowych, to forum nieco odżyje

kaszojadka: Wiem, że to stare zadanie proszę powiedzcie mi czy dobrze 1) a=6cm r=3cm

	6a2√3
Psześciokąta=		=1,5a2√3=1,5*36*√3=54√3
	4

Pole tych małych kółek ( liczę całe kółka o promieniu 3cm, jest ich 6)=πr²=9π ponieważ kąt wewnętrzny sześciokąta to 120°

	1		120
więc tego koła jest tylko		(		)
	3		360

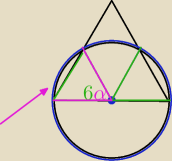
więc pole tych niecałych kółek to 3π jest ich sześć więc 18π czyli pole zacieniowanej figury to 54√3−18π 2) Pole tego koła to πr²=36π α=60° bo ten trójkącik jest równoboczny

	1
więc		pola tego koła =6π
	6

a pole tego trójkąta to 9√3 więc pole tego kawałka oznaczonego strzałką to jest 6π−9√3 połowa pola tego koła to 18π S1=18π−2(6π−9√3)=18π−12π+18√3=6π+18√3

	122√3
S2=Pcałego trójkąta−S1=		−S1=36√3−(6π+18√3)=36√3−6π−18√3=18√3−6π
	4

ite: Przyda się jeszcze: to, co nazywasz "niecałymi kółkami", ma swoją osobną nazwę − wycinek koła.

kaszojadka: ok, dzieki

kaszojadka: Obwód pierwszej figury = 12π Obwód drugiej figury= 24+2π oraz 12+2π

Mila: