tadek:
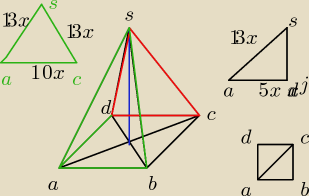
ja to rozwiązałem tak:
P|ACS| = 120
|AC| : |AS|= 10 :13
|AS| = |CS| bo to trójkąt równoramienny.
Wpierw liczę wysokość |ACS|: z twierdzenia pitagorasa
(5x)
2 + h
2 = (13x)
2
h
2= 144 x
2
h=12 x
teraz x z pola trójkąta ACS:
1/2 * 12 x * 10 x =120
60x
2 =120 /:60
x
2=2 x=
√2
obliczam boki: 13*
√2 = 13
√2
10*
√2 = 10
√2
teraz zajmuję się przekątną kwadratu:
a
√2 = 10
√2 /
√2
a= 10
obliczam pole trójkąta abs: poprzez tw pitagorasa:
a
2 + b
2 = c
2
5
2 (połowa 10) + h
2 = (13
√2)
2
h=
√313
a teraz końcówka:
Pb= 1/2 * 10 *
√313 * 4 = 20
√313
20 mar 22:06
Jakub: Sprytnie zamieniłeś długości odcinków AC i AS na 10x i 13x, wiedząc, że ich stosunek jest
10:13. To uprościło obliczenia i wyszło trochę prościej niż w moich. Patent na zastąpienie
długości odcinków, których stosunek jest podany, wyrażeniami z x, jest jak najbardziej godny
polecenia.
20 mar 22:33
tadek: Zapamiętałem to z poprzednich zadan w których Pan to pokazywał

biorę wszystkie po kolei więc się coś zapamiętuje
21 mar 20:20
kotek: wysokość to h=12x ,skoro x=
√2 to dlaczego wysokość to nie h=12
√2 
Dlaczego na nowo
obliczamy wysokość

5 lut 20:22
Kacper: 12√2 to wyskosc całego ostrosłupa.
w zadaniu potrzebujemy wysokości ściany bocznej. obliczamy ja z pitagorasa.
też zrobiłem tym sposobem. wydaje sie dużo łatwiejszy od poprzedniego.
pozdrawiam
11 kwi 21:53
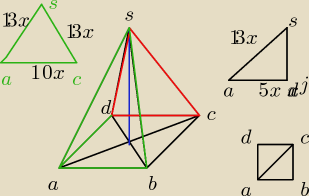 ja to rozwiązałem tak:
P|ACS| = 120
|AC| : |AS|= 10 :13
|AS| = |CS| bo to trójkąt równoramienny.
Wpierw liczę wysokość |ACS|: z twierdzenia pitagorasa
(5x)2 + h2 = (13x)2
h2= 144 x2
h=12 x
teraz x z pola trójkąta ACS:
1/2 * 12 x * 10 x =120
60x2 =120 /:60
x2=2 x=√2
obliczam boki: 13* √2 = 13√2
10* √2 = 10√2
teraz zajmuję się przekątną kwadratu:
a√2 = 10√2 / √2
a= 10
obliczam pole trójkąta abs: poprzez tw pitagorasa:
a2 + b2 = c2
52 (połowa 10) + h2 = (13√2)2
h= √313
a teraz końcówka:
Pb= 1/2 * 10 * √313 * 4 = 20 √313
ja to rozwiązałem tak:
P|ACS| = 120
|AC| : |AS|= 10 :13
|AS| = |CS| bo to trójkąt równoramienny.
Wpierw liczę wysokość |ACS|: z twierdzenia pitagorasa
(5x)2 + h2 = (13x)2
h2= 144 x2
h=12 x
teraz x z pola trójkąta ACS:
1/2 * 12 x * 10 x =120
60x2 =120 /:60
x2=2 x=√2
obliczam boki: 13* √2 = 13√2
10* √2 = 10√2
teraz zajmuję się przekątną kwadratu:
a√2 = 10√2 / √2
a= 10
obliczam pole trójkąta abs: poprzez tw pitagorasa:
a2 + b2 = c2
52 (połowa 10) + h2 = (13√2)2
h= √313
a teraz końcówka:
Pb= 1/2 * 10 * √313 * 4 = 20 √313
 biorę wszystkie po kolei więc się coś zapamiętuje
biorę wszystkie po kolei więc się coś zapamiętuje
 Dlaczego na nowo
obliczamy wysokość
Dlaczego na nowo
obliczamy wysokość 