Dociekliwy: Na samym początku w podpunkcie a) korzystasz z własności prawdopodobieństwa, ale jak to możliwe, że jesteś pewny, że zbiory A i B nie są rozłączne? Jeśli w treści nie ma takiego zapisu to mam to po prostu założyć?

Jakub: Korzystam z własności prawdopodobieństwa P(AuB) = P(A) + P(B) − P(AnB), która wcale nie zakłada, że zbiory A i B są rozłączne. Mało tego. Wyszło mi, że P(AnB) = ¹¹₃₀, więc część wspólna zbiorów istnieje.

Rafoo: jak to jest możliwe że P(AuB) = P(A) + P(B) − P(AnB), przecież suma to suma! wiec jak po odjęciu od sumy części wspólnej może to być dalej to samo? W tej części wspólnej mogły być jakieś elementy a tu się je odejmuje i dalej jest to samo, no bez sens totalny... o co chodzi ?!

ożurdłi: pomyśl jeszcze raz Rafoo

patryk:

Kinga: Mam pytanie: czy w podpunkcie a) mogę zapisać w ten sposób: P(AnB)= P(AuB) − ( P(A\B) + P(B\A) ) ? wynik jest niby ten sam ale mam watpliwosci co do poprawnosci zapisu

Jakub: Równanie, które napisałaś, jest prawdziwe. Najlepiej jednak narysować jakiś rysunek. Zaznaczyć P(AnB), P(AuB), P(A\B), P(B\A). Tak, aby było widoczne, skąd wzięłaś to równanie. Inna sprawa to, w jaki sposób to równanie ma u się do podpunktu a)? Przecież o wiele lepiej wykorzystać P(AnB) = P(A) + P(B) − P(AnB). Wystarczy tylko podstawić dane z treści zadania.

Kinga: No tak racja. Ja niestety mam zdolność do rozwiązywania zadań najdłuższym z możliwych sposobów... Dziękuje za odpowiedź

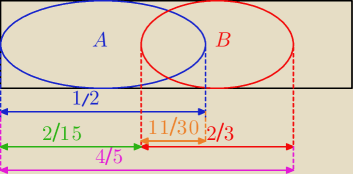
Gustlik: Najlepiej METODĄ GRAFICZNĄ, bo wzorami to jest nieprzejrzyste, nie widać, co się liczy.

	1		2		4
P(A)=		, P(B)=		, P(AUB}=
	2		3		5

Najpierw liczę P(A\B) z rysunku:

	4		2		12		10		2
P(A\B)=		−		=		−		=
	5		3		15		15		15

	1		2		15		4		11
P(A∩B)=		−		=		−		=
	2		15		30		30		30

I nie potrzeba ŻADNYCH WZORÓW, WYSTARCZY RYSUNEK !

b.: @Gustlik: Przecież to są dokładnie te same wzory, tylko zapisane za pomocą rysunku

nn:

Gustlik: b, zgadza się, ale z rysunku widzisz, co liczysz, a wzory trzeba pamiętać i jeszcze można się pomylić. Licząc samymi wzorami to taka ciuciubabka. Jakbyś sobie zawiązał oczy i liczył nie widząc, co liczysz. A tu z rysunku możesz wyprowadzić te wzory.

kl: Gustlik, nie rozumiem skąd przy liczeniu różnicy zbiorów wziąłeś 4/5? Przecież A≠AvB