Głównie to pewnie będą dowody geometryczne bo
z tym jest największy u mnie problem.
1. (0−3) PR
W trapezie ABCD o podstawach a b, poprowadzono prostą równoległą do obu podstaw, przechodzącą
przez punkt przecięcia przekątnych i przecinającą ramiona trapezu w punktach E
| 2ab | ||
i F. Wykaż, że |EF|= | . Komentarz: Próbowałem to zrobić z trójkątów podobnych i dojść | |
| a+b |
2. (0−6) PR
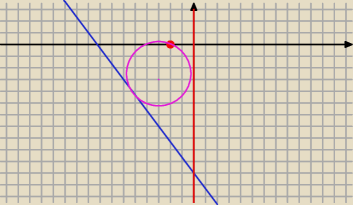
Znajdź równanie okręgu, który jest styczny zewnętrznie do okręgu (x+4)2 + (y−1)2 = 25 i
jednocześnie styczny do prostej 3x + 4y − 52 = 0. Wybierz ten z okręgów, który ma najmniejszy
możliwy promień.
Komentarz: Narysowałem podaną sytuację, ułożyłem jedno równanie ze styczności okręgów, drugie z
odległości środka szukanego okręgu od stycznej i mam za dużo niewiadomych. Zapraszam do
dyskusji.
| 3 | ||
A: y = − | x + 13 | |
| 4 |
| 4 | ||
y = | x + b | |
| 3 |
| −16 | ||
1 = | + b | |
| 3 |
| 19 | ||
b = | ||
| 3 |
| 4 | 19 | |||
y = | x + | |||
| 3 | 3 |
| 4 | 19 | |||
Więc współrzędne punktu środka naszego szukanego okręgu to S = (x, | x + | ) | ||
| 3 | 3 |
| 19 | ||
D(x)S, AU{3x + 4 * | − 52}{√32 + 42 | |
| 3 |
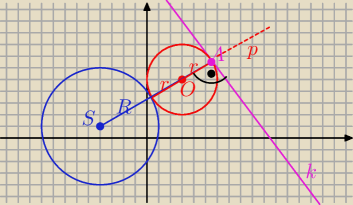k: 3x+4y−52=0
S(−4,1) , R=5
|SA|=R+2r |SA|=d −− odległość S od prostej k
zatem wyznaczysz r
O∊ p gdzie p ⊥k ...........
i |OA|=r |OA|=d −−odległość O od prostej k ⇒ wyznaczysz O
Liczyć tego,to już mi się nie chce
Właśnie zastanawiałem się czy może być tak, że te środki leżą na
jednej prostej, teraz będzie o wiele łatwiej jak to już wiem. Dziękuję
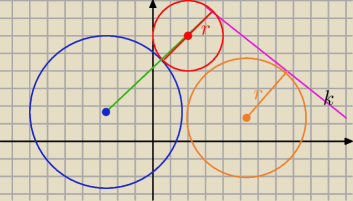Widać dlaczego najmniejsze r , to środki leżą na prostej ⊥ k
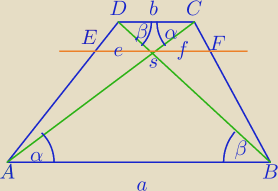EF||AB
| b | ||
1)ΔDCS∼ΔABS w skali k= | ⇔ | |
| a |
| CS | b | b | |||
= | ⇔|CS|= | |AS| | |||
| AS | a | a |
| DS | b | b | |||
= | ⇔|DS|= | *|BS| | |||
| BS | a | a |
| CS | |CS|+|AS| | b | b | ||||
= | ⇔a* | |AS|=f*|AS|*( | +1) | ||||
| f | a | a | a |
| a+b | ||
b=f* | ⇔ | |
| a |
| ab | ||
f= | ||
| a+b |
| DS | DS+BS | ||
= | ⇔|DS|*a=e*(|DS|+|BS|) | ||
| e | a |
| b | b | |||
a* | *|BS|=e*|BS|*( | +1) | ||
| a | a |
| a+b | ||
b=e* | ||
| a |
| ab | ||
e= | ||
| a+b |
| 2ab | ||
|EF|=e+f= | ||
| a+b |
Dziękuję [F[Mila] za rozwiązanie Miałem bardzo podobne rachunki, lecz za nic nie mogłem
dojść do Tej postaci tak jak Ty. Dziękuję
Bardzo Tobie Eta
dziękuje! 
Chciałbym tak szybko widzieć to samo co Wy dziewczyny
Dobra kochani, mam dalej niestety problem z zadaniem 2. (0−6) PR
Zmienne wybrane tak jak na rysunku Ety:
Prosta p prostopadła do k
| 4 | 19 | |||
p: y = | x + | |||
| 3 | 3 |
| 16 | 53 | |||
punkt A = ( | , | ) | ||
| 5 | 5 |
| 7 | ||
r = | ||
| 2 |
| 7 | |||||||||||||||||
= | ||||||||||||||||||
| √25 | 2 |
| 39 | 8 | 5 | 2 | |||||
O1 = ( | ,11 | ) lub O2 = ( | ,9 | ) | ||||
| 10 | 15 | 2 | 3 |
| 7 | ||
no i jak liczę odległość punktu O od prostej k, czyli długość odcinka AO (|AO|) to | za | |
| 2 |
2. sposób (długość odcinka AO):
| 16 | 4 | 64 | 49 | |||||
(x− | )2 + ( | x− | )2 = | |||||
| 5 | 3 | 15 | 4 |
Nie wiem co robię źle. Proszę o pomoc
| ⎧ | (x+4)2+(y−1)2=25 | |
| ⎩ | y=43x+193 |
| 165−1 | 535+5 | 11 | 78 | |||||
O = SAL = ( | , | ) = ( | , | ) | ||||
| 2 | 2 | 10 | 10 |
| 11 | 53 | |||
x= | ∨ x= | , masz błędy rachunkowe... jedną odpowiedź odrzucamy, bo nie będzie | ||
| 10 | 10 |
bo 5 i jeszcze prawie pół piątki
| 11 | 39 | 49 | ||||
Więc ostatecznie równanie jedynego słusznego okręgu to: (x− | )2+(y− | )2= | ||||
| 10 | 5 | 4 |
Przecież u mnie jedna kratka to jedna jednostka, a to nie jest to samo co 1 cm
Stary i głupi
Dziękuje Qulka i chichi Pół dnia na to zadanie poświęcone i już w końcu z głowy
https://cke.gov.pl/informacje-o-testach-diagnostycznych-probny-egzamin-osmoklasisty-i-maturalny/?fbclid=IwAR1x6aMfJLs006FdpDG6OphGeFsFuSgBh5oExJvC4hqf4V7t99mJP1wo4sQ
A niedługo matury próbne CKE, już nie mogę się doczekać
| |253x−803| | 7 | ||
= | |||
| 5 | 2 |
| 11 | 53 | |||
|10x − 32| = 21 ⇔ x1 = | u x2 = | |||
| 10 | 10 |
| 1 | 8 | 3 | 2 | |||||
O1 = (1 | ,7 | ) u O2 = (5 | ,13 | ) | ||||
| 10 | 10 | 10 | 5 |
https://matematykaszkolna.pl/forum/406969.html
