Dany jest ciąg
Julia: Dany jest ciąg an=an2+bn+c, dla n€N+
Oblicz ilość wyrazów ujemnych tego ciągu.
a=2 b=4 c=−70
16 lut 18:00
Filip:
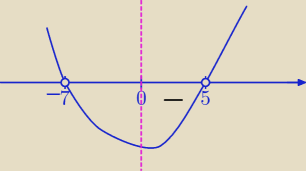
n2 + 2n − 35 < 0
n2 − 5n + 7n − 35 < 0
n(n − 5) + 7(n − 5) < 0
(n − 5)(n + 7) < 0
−7 < n < 5
16 lut 18:12
Mila:
an=2n2+4n−70
2n2+4n−70<0 i n∊N+
rozwiąż
16 lut 18:13
Emilia: Nie rozumiem jak dalej to zrobić
16 lut 19:05
Emilia: Odpowiedź to 4?
16 lut 19:15
?: Ale przecież to
Julia zadała pytanie
Nie potrafisz rozwiązać nierówności kwadratowej? A zwykłe równanie rozwiążesz?
2n
2 + 4n − 70 = 0
16 lut 19:16
?: 19:15 − Tak, to poprawna odpowiedź
16 lut 19:17
Mila:
2n
2+4n−70<0 i n∊N+
Δ=16+4*2*70=576=24
2
| | −4−24 | | −4+24 | |
n1= |
| =−7 lub n2= |
| =5n |
| | 4 | | 4 | |
n∊(−7,5) i n∊N
+
⇔ujemne wartości mają wyrazy:
a
1,a
2,a
3,a
4
możesz obliczyc
16 lut 19:19